Let $ABCD$ be a convex quadrilateral. If the measure of the angles $A=90, C=96, D=78$ and $BC=2*AB$, then the measure of the angle $ABD$ is?

Question

The problem

Let $ABCD$ be a convex quadrilateral. If the measure of the angles $A=90°, C=96°, D=78°$ and $BC=2*AB$, then the measure of the angle $ABD$ is...?

The idea

As you can see I calculated above $B$ as $96$.Let point $X$ be the midpoint of $BC$ and then we got the isosceles triangle $BAX$.

I also looked for inscribed quadrilaterals but found none.

I Hope one of you can help me with a non trigonometric proof! Thank you!

Answer 1

Start with a regular pentagon $P_1 P_2 P_3 P_4 P_5$ ($P_1\equiv D$), and an equilateral triangle $P_1 P_2 B$ (see Figure below). Let $C$ be the point inside the pentagon giving $\measuredangle C P_1 P_2 = \measuredangle CP_2P_1 = 6^\circ$. Finally, drop from $P_1$ the perpendicular to $P_5 B$, and let $A$ be its intersection with this segment. We want to show that $ABCD$ has the desired properties. Angle chasing easily shows that the internal angles of this quadrilateral are as in the hypotheses. It suffices then to show that $BC \cong 2AB$, or, equivalently, that $P_5 B \cong BC$.

To this aim, extend $P_5 P_1$ to $F$ so that $P_1FC$ is isosceles. Since $\measuredangle CP_1F = 78^\circ$, we have that $P_1CF = 24^\circ$. Construct now the equilateral triangle $P_3P_5E$. Angle chasing gives $\measuredangle P_2P_1E = 42^\circ$ (hint: use the fact that $P_1P_3E$ is isosceles and determine its internal angles...), which results in $P_1CE$ being isosceles with $\measuredangle P_1CE = 84^\circ$. Therefore $FCE$ is equilateral. Angle chasing on $P_5FE$, gives that $\measuredangle P_5EF = 30^\circ$. Therefore $P_5FEC$ is a kite, with $\measuredangle FP_5C = 24^\circ$. Again angle chasing allows to obtain that $P_5CB$ is isosceles, which is our thesis. The result $$\boxed{\measuredangle ABD = 66^\circ}$$ is a trivial consequence of the construction.

---

EDIT A faster proof is as follows.

The quadrilateral $ABCD$ can be carved out from the figure depicted below, where $P_1P_2P_3P_4P_5$ is a regular pentagon ($P_2\equiv C$) and $P_3P_5B$ is an equilateral triangle, with line $CD$ perpendicularly bisecting $P_4P_5$, and $P_3A \perp P_1B$. Note in fact (as in the proof above) that $P_1P_3B$ is isoceles with $\measuredangle P_1P_3B = 24^\circ$. Hence $\measuredangle P_3P_1B = 78^\circ$ and $\measuredangle CP_1B = \measuredangle P_1CB = 42^\circ$. Being $P_1 P_3 B$ isosceles, we also have that $P_3A$ perpendicularly bisects $P_1B$, whence $BC \cong 2AB$. Finally, the fact that $CD$ perpendicularly bisects $P_4P_5$ guarantees $\measuredangle BCD = 42^\circ + 54^\circ = 96^\circ$, as desired.

Now, $CD$ perpendicularly bisects $P_1P_3$. Therefore $P_1P_3D$ is isoseles. Hence $\measuredangle DP_1P_3 = 12^\circ$. We have, as a consequence, that $\measuredangle DP_1B = 66^\circ$, the thesis following from the fact that $P_1DB$ is isosceles as well.

Answer 2

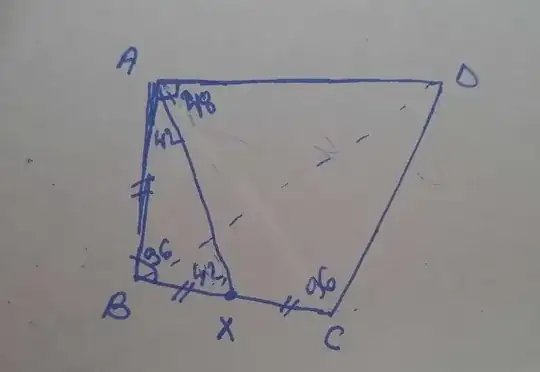
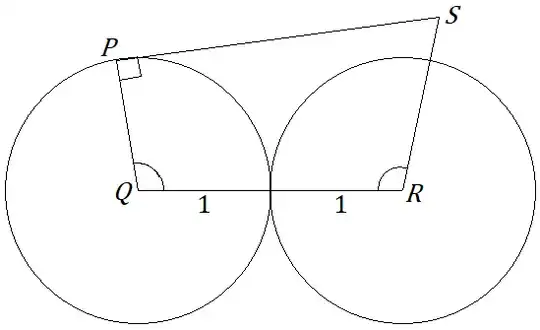
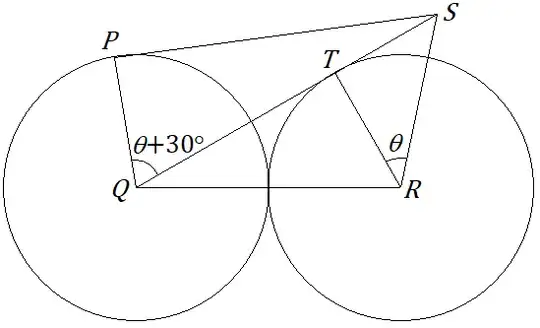
Notice that $BC=2AB$, $\angle A=90^\circ$, let's find the perpendicular bisector of $BC$. 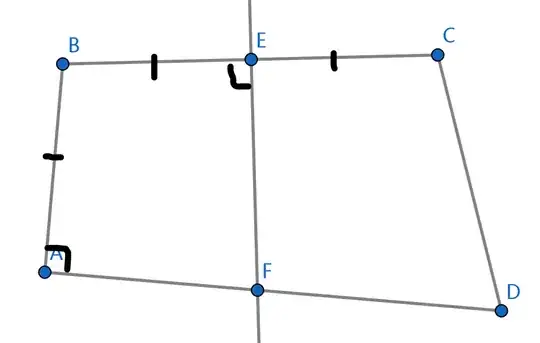Now we have that $B$ and $C$ are symmetric w.r.t $EF$, and $A$ and $E$ are symmetric w.r.t $BF$. If we extend $AB$ and $DC$, they will intersect $FE$ at the same point, and both make a $6^\circ$ angle. If we extend $CB$ and $DA$, they will make a $6^\circ$ angle as well.

The angle can be found by trigonometry straightforwardly. Let $AB$, $FE$, $DC$ intersect at $Q$. Let $\tan\theta=\tan\angle ABD=\frac{AD}{AB}$.

We have $\frac{AD}{AQ}=\tan 12^\circ$, $\frac{AQ}{AB}=1+\frac{BQ}{AB}=1+\frac{BQ}{BE}=1+\frac{1}{\sin 6^\circ}$. Solve for $\theta$,

$\tan \theta=\frac{AD}{AB}=\tan 12^\circ(1+\frac{1}{\sin 6^\circ})$

$\theta=66^\circ$.

This is probably the best way to find the angle. But the proof can avoid using trigonometry, as the following.

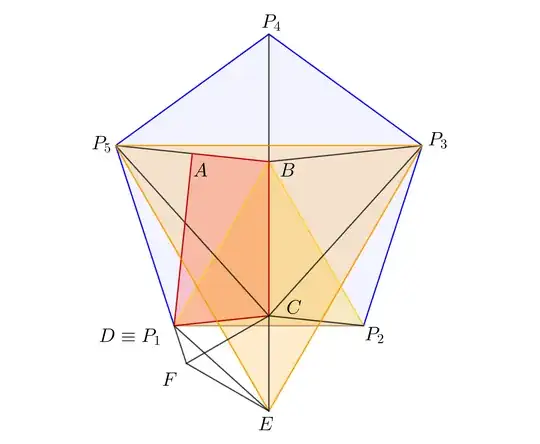
What if we extend all these lines... and draw more to complete an equilateral triangle? 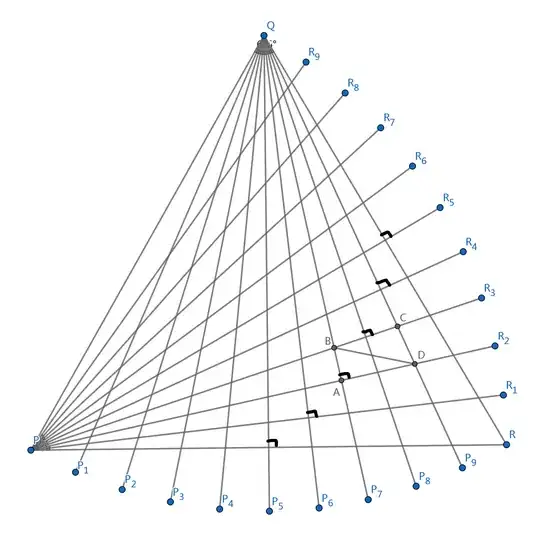We have an equilateral triangle $\triangle PQR$, and all the $60^\circ$ angles are cut into $6^\circ$ pieces. The location of the quadrilateral $ABCD$ is shown on the graph.

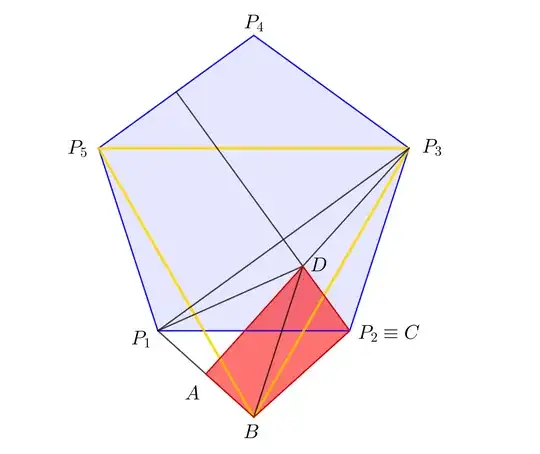
To find $\angle ABD$, we can use symmetry to move it to a different location: 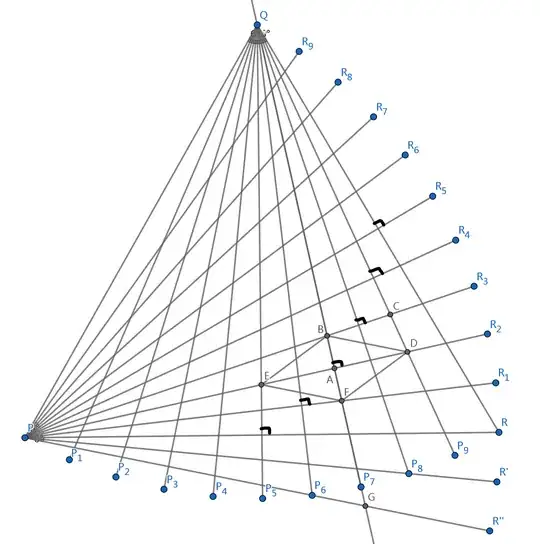Due to symmetry w.r.t $QP_7$ and symmetry w.r.t $PR_2$, $BD=BE=EF=FD$. So, $\angle ABD=\angle AFE$.

We want to prove that $\angle AFE=66^\circ$, or, $\angle AEF=24^\circ$. Is there a line that makes a $24^\circ$ angle with $AE$?

Yes, if we just add two more lines, $PR'$ and $PR''$, we have that $\angle APR''=4\times 6^\circ=24^\circ$, so we just need to prove that $EF\parallel PR''$.

---

If we try $\frac{AE}{AP}=\frac{AF}{AG}$, then this can be converted to a tangent identity. $\frac{AE}{AP}=\frac{AE}{AQ}\frac{AQ}{AP}=\frac{\tan 12^\circ}{\tan 42^\circ}$, $\frac{AF}{AG}=\frac{AF}{AP}\frac{AP}{AG}=\frac{\tan 6^\circ}{\tan 24^\circ}$. Thus we must have $\frac{\tan 12^\circ}{\tan 42^\circ}=\frac{\tan 6^\circ}{\tan 24^\circ}$, or

$\tan 12^\circ \tan 24^\circ \tan 48^\circ \tan 84^\circ = 1$,

This is one of the 15 independent four element integer degree tangent identities, which I spent some time trying to understand before.

It's pretty cool to see the connection here, but I'm not going to discuss it any further. Let's go back to the geometry proof.

---

Is there another way to get a $24^\circ$?

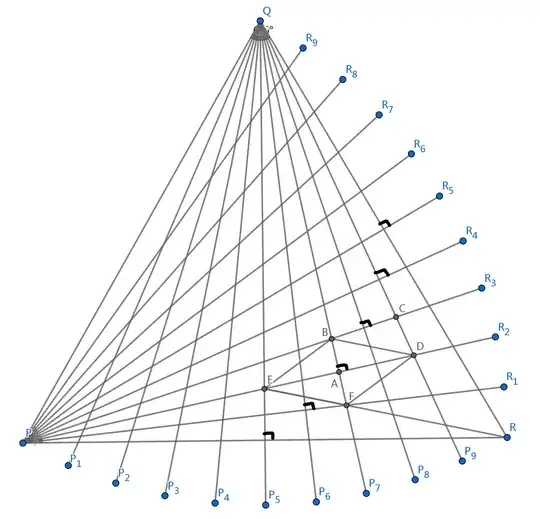
Noticing that $\angle APR=12^\circ$, and $P$ and $R$ are symmetric w.r.t $QE$, so $\angle ERP=12^\circ$ as well. Now, if $F$ is on line $ER$, then it's done, $\angle AEF=24^\circ$!

But how do we prove that $E,F,R$ are on the same line?

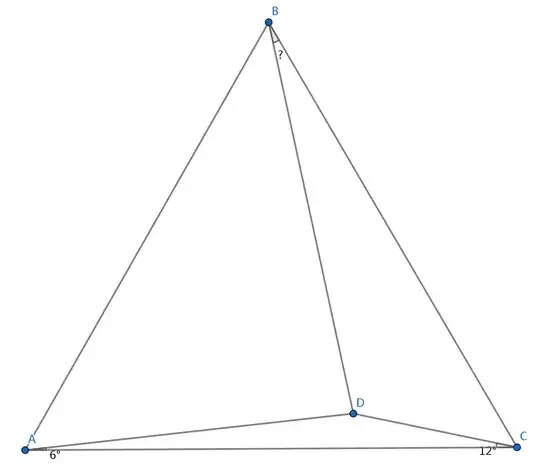
Now we can convert it to another problem, a classic:

Given equilateral triangle $ABC$, $D$ is inside the triangle, $\angle DAC=6^\circ$, $\angle DCA=12^\circ$. Prove that $\angle CBD=18^\circ$.

There are a few other equivalent formularizations, and there are many solutions. One of them goes as the following:

Find the point $E$ such that $\angle EAD=\angle EDA=6^\circ$. So $EA=ED$.

$ED\parallel AC$, so $AE=CD$.

Find point $F$ and $G$ so that $EF=EA, DG=DC$.

So, $\angle AFE=\angle FAE=48^\circ$, $\angle FED= 2\times 48^\circ+2\times 6^\circ=108^\circ$, $\angle EFD=\angle EDF=36^\circ$. $\angle DGC=\angle DCG=48^\circ$.

$AF=CG$, so $BF=BG$, $BFG$ is equilateral. $FG\parallel DE$, so $\angle GFD=\angle FDE=36^\circ$. $\angle FGD=180^\circ-60^\circ-48^\circ=72^\circ$. So, $\angle FDG=180^\circ-36^\circ-72^\circ=72^\circ=\angle FGD$, $FD=FG$.

So, $FD=FB$, $\angle FBD=\frac{1}{2}\angle AFD=\frac{1}{2}(48^\circ+36^\circ)=42^\circ$, $\angle CBD=18^\circ$. The proof is complete.

---

One extra fact:

54,6,12,48,18,42 is not the only non-trivial combination that fits in an equilateral triangle. Another one is 54,6,18,42,12,48. And, no, this is not a duplicated combination. Changing the order gives a different problem, and there're quite a few solutions for this problem, too.

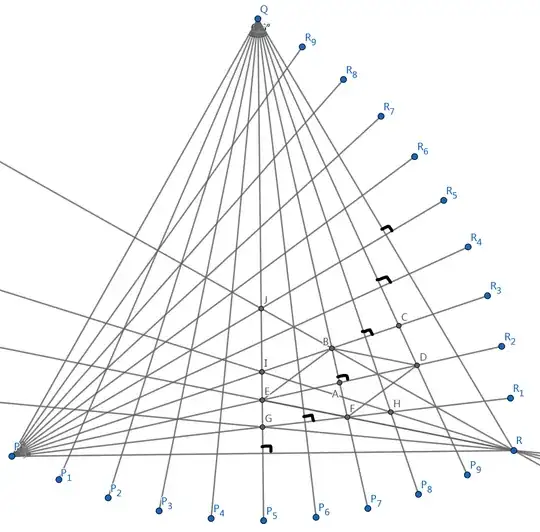On the triangle figure, it implies that, the point $H$ lies on the line $RI$. Quite intriguing facts!

Answer 3

The OP expressed preference for a non-trig proof, but I am posting the following trig proof because I think it is simpler than the non-trig proofs given so far.

---

Start with tangent unit circles $C_Q$ and $C_R$ with centres $Q$ and $R$, respectively.

Point $P$ is chosen somewhere on $C_Q$. Then point $S$ is located so that $\angle SPQ=90^\circ$ and $\angle PQR=\angle SRQ$.

We will show that if $\overline{QS}$ is tangent to $C_R$, then quadrilateral $PQRS$ is similar to quadrilateral $ABCD$ in the question. Then $\angle ABD$ must equal $\angle PQS$, which will be easy to find.

---

Assume that $\overline{QS}$ is tangent to $C_R$ at point $T$. Let $\angle SRT=\theta$. Then $\angle PQT=\theta+30^\circ$.

$QS=\dfrac{1}{\cos (\theta+30^\circ)}$ and $QS=QT+TS=\sqrt3+\tan\theta$

$\therefore \dfrac{1}{\cos (\theta+30^\circ)}=\sqrt3+\tan\theta$

$\left(\frac{\sqrt3}{2}\cos\theta-\frac12\sqrt{1-\cos^2\theta}\right)\left(\sqrt3+\frac{\sqrt{1-\cos^2\theta}}{\cos\theta}\right)=1$

$4\cos^2\theta-2\cos\theta-1=0$

$\cos\theta=\dfrac{1+\sqrt5}{4}$

Therefore $\theta=36^\circ$

This implies $\angle PQR=\angle SRQ=96^\circ$, and $\angle PSR=78^\circ$. Thus, quadrilateral $PQRS$ is similar to quadrilateral $ABCD$ in the question. Thus, $\angle ABD=\angle PQS=\theta+30^\circ=\boxed{66^\circ}$.

Answer 4

Let $AB = 1$, then $BC = 2$. Also, let $AD = x$ and $CD = y$. We know that

$ \angle A = 90^\circ , \angle C = 96^\circ , \angle D = 78^\circ $ so $\angle B = 360^\circ - 90^\circ - 96^\circ - 78^\circ = 96^\circ$.

Using the law of cosines, we have for the two diagonals,

$ AC^2 = 1^2 + 2^2 - 4 \cos 96^\circ = x^2 + y^2 - 2 x y \cos 78^\circ $

$ BD^2 = 1^2 + x^2 - 2 x \cos 90^\circ = 2^2 + y^2 - 4 y \cos 96^\circ $

Solving these two quadratic equations in $x$ and $y$ gives us

$x = 2.246037 , y = 1.236068 $

Now, for $\triangle ABD$, we have

$ BD = \sqrt{ 1^2 + x^2 - 2 x \cos 90^\circ } = 2.458593 $

Finally, by the law of sines in $\triangle ABD$

$\sin \angle ABD = \sin 90^\circ \left( \dfrac{ x }{ BD } \right) = 0.913545 $

Hence, $\angle ABD = \sin^{-1}( 0.913545 ) = 66^\circ$

Answer 5

This replaces an earlier unsatisfactory attempt with one somewhat similar to @dfnu.

Let $FE$, $ED$ be sides of a regular $30$-gon, so that $\angle FED=168^o$.

Construct an equilateral triangle on $FE$, a regular pentagon on $ED$, and join $FD$, $FL$, $FJ$. Thus $\angle EDF=\angle DFE=6^o$.

Let $EB$ bisect $\angle FED$, make $BC\parallel ED$, construct $\angle EDC=\angle BED=84^o$, and join $BD$, $EC$.

Thus $EB\perp FD$ and $\angle EBC=\angle DCB=96^o$. Since$$\angle KFH=\frac{1}{2}(60^o-2\cdot6^o)=24^o$$then by similar triangles$$\angle FKH=\angle EKA=\angle EBH=\angle DBA=66^o$$And since the vertices of isosceles trapezoid $EDCB$ are concyclic, then$$\angle ECB=\angle CBD=96^o-66^o=30^o$$Make $BN\perp EC$. Then in triangle $BNC$, $BN=\frac{1}{2}BC$, and since $APNB$ is a kite, then$$AB=BN=\frac{1}{2}BC$$and $ABCD$ is the given figure.