When analyzing one dimensional diffusion processes it is essential to construct the eigen-functions of the infinitesimal generator ${\mathfrak G}_z$ of the process. It turns out that there is always a pair of linearly independent functions both being positive and one being strictly increasing and the other one being strictly decreasing, which span the space of eigen-functions of the generator (see page 130 in 1). Those eigen-functions are necessary for constructing the transition probability density function of the process in question (see section 4.11, pages 149-160 in 1) as well as finding the first hitting time distribution of that process (see section 4.6 pages 128--134 in 1)
Now, in my previous post, we were trying to find those eigen-functions, i.e. solutions to the ODE ${\mathfrak G}_z u_\lambda(z) = \lambda u_\lambda(z)$ with $\lambda \ge 0$, for the diffusion $d X_t = \mu X_t^\beta dt + \sigma X_t d B_t$ subject to $X_0=x$ with $B_t$ being the Brownian motion. The eigen-functions read as follows:
\begin{eqnarray} u^{(1,2)}_\lambda(z):=\left\{z^{(\beta -1) a_{\lambda }} \, _1F_1\left(a_{\lambda };b_{\lambda };x_z\right),z^{(\beta -1) a_{\lambda }} U\left(a_{\lambda },b_{\lambda },x_z\right)\right\} \tag{1} \end{eqnarray} where $a_\lambda:= 1/(1-\beta) \left( -1 + (\sigma + \sqrt{8 \lambda+\sigma^2})/(2 \sigma)\right)$, $b_\lambda:= 1+ \sqrt{8 \lambda +\sigma^2}/(\sigma (1-\beta))$ and $x_z:= 2 \mu/((1-\beta) \sigma^2) z^{-1+\beta}$. Here $\beta <1$.
Now, it is fairy straightforward to show that the first eigen-function in $(1)$ is strictly decreasing. Indeed, by direct differentiation, we have $d/dz u^{(1)}(z) = (-1) z^{-1+(-1+\beta) a_\lambda} (1-\beta) a_\lambda \, _1F_1\left( 1+a_\lambda,b_\lambda,x_z\right) < 0 $. This follows from the integral representation of the confluent hypergeometric function and the fact that $a_\lambda >0$, $b_\lambda >0$ and $b_\lambda - a_\lambda -1 >0$.
However, for the second function things get more complicated. We have $d/dz u^{(2)}(z) = z^{-1+(-1+\beta) a_\lambda} a_\lambda (1-\beta) \left(-U\left( a_\lambda, b_\lambda,x_z\right) + x_z U\left( 1+a_\lambda, 1+b_\lambda,x_z\right)\right) $.
After this lengthy introduction we can finally formulate our question. Let $a >0$, $b > 1+a$ and $x >0$. How do we prove or disprove the following conjecture:
Conjecture:
\begin{equation} {\mathfrak g}_{a,b}(x): = -U\left( a, b,x\right) + x U\left( 1+a, 1+b,x\right) >0 \tag{2} \end{equation}
What have we achieved so far?
For small values of $x$ the function in $(2)$ reads as follows $ {\mathfrak g}_{a,b}(x) \simeq x^{1-b} \cdot (b-a-1)/a \cdot \Gamma(b-1)/\Gamma(a) > 0 $ for $ x \rightarrow 0_+$. This follows from the definition of the function $u$ as a linear combination of two confluent hypergeometric function (see Wiki page on the confluent hypergeometric function). For big values of $x$ the function in question reads $ {\mathfrak g}_{a,b}(x) \simeq x^{-1-a} (b-a-1) > 0 $ for $x \rightarrow \infty$. this follows from the asymptotic expansion in Wolfram's site.
Now, by direct differentiation it turns out that $d^n/dz^n {\mathfrak g}_{a,b}(x) = (-1)^n (1+a)^{(n)} g_{a+n,b+n}(x)$ for $n=1,2,3,\cdots$ and therefore the function in question can be expanded in a Taylor series about unity as follows:
\begin{equation} {\mathfrak g}_{a,b}(x) = \sum\limits_{n=0}^\infty (1+a)^{(n)} \left( -U(a+n,b+n,1) + U(a+n+1,b+n+1,1)\right) \frac{(1-x)^n}{n!} \tag{3} \end{equation}
Now, if we only assume that ${\mathfrak h}_{a,b}:=-U(a,b,1) + U(a+1,b+1,1) >0 $ for every $a>0$ and $b > a+1$ then, from $(3)$, we have proven our conjecture for every $0 < x \le 1$ (Why? Because all the terms in the infinite sum are positive.)
Now, there are some numerical verifications. Firstly that of identity $(3)$. Here we go:
In[2478]:= a = RandomReal[{0, 1}, WorkingPrecision -> 50];
b = RandomReal[{1 + a, 3}, WorkingPrecision -> 50];
xx = RandomReal[{0, 1}, WorkingPrecision -> 50]; MM = 100;
(* xx^(1-b)( (b-a-1)/a ) Gamma[b-1]/Gamma[a] for xx-->0_+ from
definition
https://en.wikipedia.org/wiki/Confluent_hypergeometric_function)
( xx^(-1-a) (b-a-1) for xx-->Infinity from asymptptic
expansion see
https://functions.wolfram.com/HypergeometricFunctions/HypergeometricU/
06/02/*)
Take[Accumulate[
Table[Pochhammer[1 + a,
n] (-HypergeometricU[n + a, n + b, 1] +
HypergeometricU[n + 1 + a, n + 1 + b, 1]) (-xx + 1)^n/n!, {n,
0, MM}]], -5] // MatrixForm
(- HypergeometricU[a, b, xx] + xx HypergeometricU[1 + a, 1 + b, xx] )
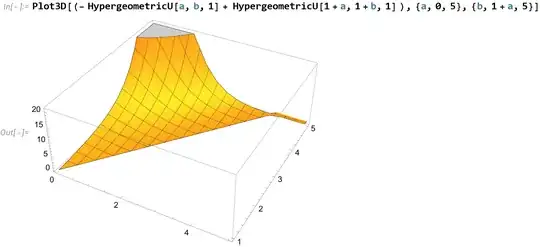
Now we plot the ${\mathfrak h}_{a,b}$ function below and we indeed see that it is positive and that it hits zero when $b=1+a$. Here we go:
So , on the face of it, we have proven our conjecture for all $0< x \le 1$.
Having said all this my question would be, firstly how do we finish the proof and secondly, is there a simpler and more elegant way of proving our conjecture?
1: Itô, Kiyosi; McKean, Henry P. jun., Diffusion processes and their sample paths., Classics in Mathematics. Berlin: Springer-Verlag. xviii, 326 p. (1996). ZBL0837.60001.