limit of diagram of limits can be check in the category of sets?

Question

I got that the following diagram \begin{equation*} \require{AMScd} \begin{CD} X_1\times_Y X_2 @>>> X_1\times_Z X_2\\ @V V V @VV V\\ Y @>>> Y \times_Z Y \end{CD} \end{equation*} being pullback can be checked in the category of sets from The "magic diagram" is cartesian and it also holds for the following diagrams (Quoted from Görtz&Wedhorn’s algebraic geometry):

Definition 9.1 Let $\mathscr{C}$ be a category and $X, Y, S$ be objects in $\mathscr{C}$, and $u: X \rightarrow S$, $v : Y \rightarrow S$, $f: X \rightarrow Y$ be three morphisms that commute, (i.e., $f : X \rightarrow Y$ is a morphism of $S$-objects). The morphism $$ \Gamma_f := (\operatorname{id}_X, f)_S : X \rightarrow X \times_S Y $$ i.e, induced by the following diagram

is called the diagram (morphism) of $f$.

Proposition 9.3 Let $u: X \rightarrow S, v :Y \rightarrow S$ be $S$-objects, let $p: X \times_S Y \rightarrow X$ and $q : X \times_S Y \rightarrow Y$ be the projections, and $f, g: X \rightarrow Y$ two $S$-morphisms. Then

(2) All rectangles of the the following diagram are cartesian.

(3) Let $s: S \rightarrow X$ be a section of $u$ (i.e., $u \circ s = \operatorname{id}_S$). The following diagram is cartesian.

But the following diagram is also cartesian from a Lean’s definition:

Given $f : X \rightarrow Y, i: U \rightarrow Y$ and $i_1: V_1 \rightarrow X \times_Y U, i_2: V_2 \rightarrow X \times_Y U$, the following diagram is cartesian:

an auxiliary diagram for this is:

I am wondering how general is result like this hold, like the Freyd-Mitchell embedding theorem for abelian category. At first I am thinking it should be diagram about limits of the same shape. But some of them seems not following this pattern.

Answer 1

$\require{AMScd}$As commented, all functors of type $\hom(X,-)$ preserve limits (corepresentable functors are continuous). But we need more than that! We need its partial converse. Fix a locally small category $\mathscr{C}$ - then:

If $\mathfrak{D}:\mathscr{J}\to\mathscr{C}$ any small diagram, then a cone in $\mathscr{C}$ over $\mathfrak{D}$, $(\ell,\tau:\Delta\ell\implies\mathfrak{D})$, is a limit of $\mathfrak{D}$ if and only if for all objects $\varsigma\in\mathscr{C}$, the cone obtained by applying $\mathscr{C}(\varsigma,-)$ to everything, $(\mathscr{C}(\varsigma,\ell),\tau_\ast)$, is a limit for the diagram $\mathscr{C}(\varsigma,\mathfrak{D}(-)):\mathscr{J}\to\mathsf{Set}$.

If you know about the pointwise evaluation theorem, this can be rephrased as follows:

The Yoneda embedding $y:\mathscr{C}\hookrightarrow[\mathscr{C}^{\mathsf{op}},\mathsf{Set}]$ preserves and reflects (but does not necessarily create, I don't think) limits of small diagrams.

This is a useful very general theorem. The idea is that, morally, the Yoneda embedding is, well, an embedding; you can really view $\mathscr{C}$ as inside the presheaf category and somehow properties you care about translate into properties within the presheaf category.

To prove the fact; assuming $(\ell,\tau)$ is a limit, the explicit construction of limits in the category of sets makes the proposition clear. Arrows $\varsigma\to\ell$ really are the same thing as cones over $\mathfrak{D}$ which really are the same thing as families of compatible elements of $\mathscr{C}(\varsigma,\mathfrak{D}(-))$. In the converse - which is what you need now, with Gortz-Wedhorn - you must check $(\ell,\tau)$ has the intended universal property... and what does that really mean? Well, you have to take any arbitrary $X$ and then say something about cones with apex $X$ versus arrows $X\to\ell$ and everything you need would follow from the assertion that $(\mathscr{C}(X,\ell),\tau_\ast)$ is a limit for $\mathscr{C}(X,\mathfrak{D}(-))$. The universal property quantifies $\forall X$ so to check it you can just instantiate at any particular $X$ and use the pointwise hypothesis.

Explicitly, say you have a square in the category: $$\begin{CD}A@>f>>B\\@VgVV@VVhV\\C@>>e>D\end{CD}$$And you want to check it is Cartesian. You don't a priori even need to assume it commutes. Gortz-Wedhorn are saying it suffices to check this square is Cartesian once an arbitrary $\hom(X,-)$ is applied. By applying $\hom(A,-)$ and testing on $1_A$ in the top left corner, you immediately realise the original square commutes since the square of hom-sets is supposed to commute. Ok - now we must check the universality. That means, if $X$ is any object, we need to check that arrows $c:X\to C,b:X\to B$ such that $ec=hb$ factor as $c=ga,b=fa$ for a unique $a:X\to A$.

Well, sure - let $X$,$c$,$b$ be an example of the above situation. We know that: $$\begin{CD}\hom(X,A)@>f_\ast>>\hom(X,B)\\@Vg_\ast VV@VVh_\ast V\\\hom(X,C)@>>e_\ast>\hom(X,D)\end{CD}$$Is Cartesian. There is a set $S:=\hom(X,X)$ and functions $b_\ast:S\to\hom(X,B),c_\ast:S\to\hom(X,C)$ with $e_\ast c_\ast=h_\ast b_\ast$ so there is a unique function $\alpha:S\to\hom(X,A)$ with $f_\ast\circ\alpha=b_\ast,g_\ast\circ\alpha=c_\ast$ by the Cartesian property. If $a:=\alpha(1_X)$ then we know $b=fa,c=ga$ immediately. It remains to check $a$ is unique with this property; but any solution $a$ to those equations would make a function $\alpha:=a_\ast$ which satisfies the equations given above and as this is unique - since we assume the square of hom-sets is Cartesian - the uniqueness of $a$ is immediate, $a_\ast=a'_\ast$ implying $a=a'$ since you can just plug in the identity.

Answer 2

Suppose we already have the following result:

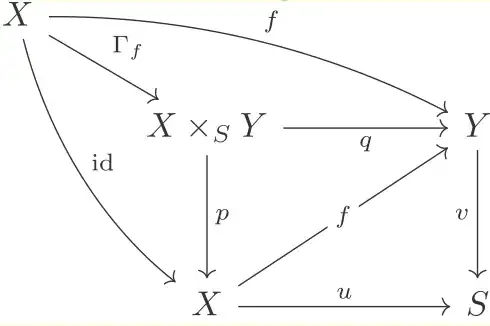
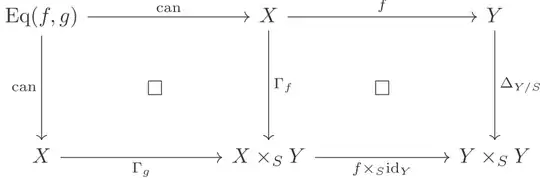
Given any sets $X, Y, S$ and maps $u : X \rightarrow S, v: Y \rightarrow S$ between them, and $S$-maps $f, g: X \rightarrow Y$, i.e., $u = v \circ f = v \circ g$. Then the following diagram is cartesian (i.e., pullback diagram): \begin{equation*} \begin{CD} \operatorname{Eq}(f, g) @>{\operatorname{can}}>> X\\ @V\operatorname{can} V V @VV\Gamma_f V\\ X @>>\Gamma_g> X \times_S Y \end{CD} \end{equation*}

We want to show that (just replace the words sets/maps to objects/morphisms):

Given any objects $X, Y, S$ in a category $\mathscr{C}$ and morphisms $u : X \rightarrow S, v: Y \rightarrow S$ between them, and $S$-morphisms $f, g: X \rightarrow Y$, i.e., $u = v \circ f = v \circ g$. Then the aobve diagram is also cartesian (i.e., pullback diagram).

Given any $A \in \operatorname{Obj}\mathscr{C}$, applying the coyoneda functor $h_A$ (Here we reuse the variable names $f,g$): \begin{equation*} \begin{cases} X \mapsto \operatorname{Hom}(A, X) \\ X \xrightarrow[]{f} Y \mapsto (A \xrightarrow[]{g} X \mapsto f \circ g) \end{cases} \end{equation*} on all the above data, we have sets $h(X), h(Y), h(S)$ and maps $h(u): h(X) \rightarrow h(S), h(v): h(Y) \rightarrow h(S)$, and $h(S)$-maps $h(f), h(g): h(X) \rightarrow h(Y)$ (Here we omit the subscript letter $A$ when there is no confusion). Hence applying the assumption, the following diagram is cartesian: \begin{equation*} \begin{CD} \operatorname{Eq}(h(f), h(g)) @>{\operatorname{can}}>> h(X)\\ @V\operatorname{can} V V @VV\Gamma_{h(f)} V\\ h(X) @>>\Gamma_{h(g)}> h(X) \times_{h(S)} h(Y) \end{CD} \end{equation*} Now we should manuplate the above diagram "to commute the limit operations and (co)yoneda applications" (That's why I think it's kind of fuzzy for the general result and it must be handled case by case. Although generally it's from the fact that the yoneda functor preserves limit, but different diagrams seem given different proof here. And it seems hard to make a general statement.) Namely, we want the following diagram that can conclude the statement we want (from the fact that the yoneda functor reflects limit): \begin{equation*} \begin{CD} h(\operatorname{Eq}(f, g)) @>{h(\operatorname{can})}>> h(X)\\ @Vh(\operatorname{can}) V V @VV h(\Gamma_f) V\\ h(X) @>>h(\Gamma_g)> h(X \times_S Y) \end{CD} \end{equation*} From the construction of limits in the category of sets, $\operatorname{Eq}(h(f), h(g))$ is isomorphic to $$ \left\{x \in h(X) : f \circ x = g \circ x \right\} $$ But it's isomorphic to the set $h(\operatorname{Eq}(f, g))$. Similarlly we have $h(X) \times_{h(S)} h(Y)$ is isomorphic to the set $h(X \times_S Y)$. (Here we use the word "isomorphic" but not "equal" for respecting the fact that limits are only determined up to unique isomorphism and being very detailed.)

Now we have the following diagram (all askew maps are isomorphisms). We a priori still don't know that the four trapezoidal diagrams are commute. Next we prove this, from which the outer square does be commute and cartesian.

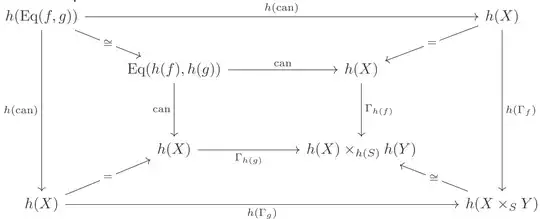
But from the definition for the isomorphism $\operatorname{Eq}(h(f), h(g)) \cong h(\operatorname{Eq}(f, g))$, it's deriven from the following diagram:

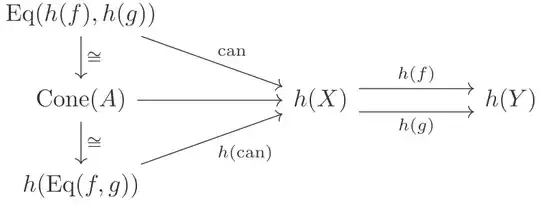
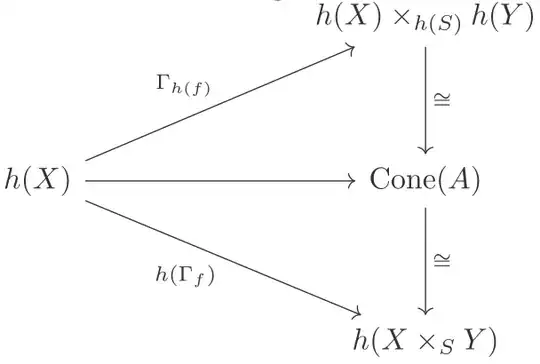
The isomorphism factored from the top triangle diagram is from the fact that limits are unique up to unique isomorphism, and the bottom triangle diagram is commute for its explicit construction: any element (i.e. cone, here just some morphism $x : A \rightarrow X$) is taken to $x$ itself via the morphism $\operatorname{Cone}(A) \rightarrow h(X)$ (the projection), and $\operatorname{Cone}(A) \xrightarrow[]{\cong} h(\operatorname{Eq}(f, g))$ takes $x$ to some $y: A \rightarrow \operatorname{Eq}(f, g)$ in $h(\operatorname{Eq}(f, g))$, and then $h(\operatorname{can}): h(\operatorname{Eq}(f, g)) \rightarrow h(X)$ takes it to $h(\operatorname{can})\circ y$, which is same as $x$. (Here there is some mess up with the notation $\operatorname{can}$: it used for both the canonical morphism for the equalizer $f, g: X \rightarrow Y$ and $h(f), h(g): h(X) \rightarrow h(Y)$). Hence the top trapezoidal does be commute. Similar argument can be applied for others, say the right trapezoidal diagram:

Here $\operatorname{Cone}(A)$ is used for denoting the set of all cones with vertex $A$: \begin{equation*} \begin{CD} A @>>> Y\\ @V V V @VV V\\ X @>>> S \end{CD} \end{equation*} And similarly the top triangle diagram commutes for the uniqueness of limits. And bottom triangle diagram commutes for its explicit construction: any element $x: A \rightarrow X$ in $h(X)$ is taken to the cone $\{x: A \rightarrow X, f \circ x: A \rightarrow Y\}$ by the map $h(X) \rightarrow \operatorname{Cone}(A)$ (recall that $v \circ f = u$):

and then the isomorphism $\operatorname{Cone}(A) \xrightarrow[]{\cong} h(X \times_S Y)$ takes the cone here to some factored morphism $y: A \rightarrow X \times_S Y$. But this is same as $\Gamma_f \circ x$ for the uniqueness of the factored morphism, which is the image of $x$ under $h(\Gamma_f)$.

From the above argument we do have all trapezoidal diagrams commute. And hence the outer square commute. And hence the original diagram in the category $\mathscr{C}$ is commute, for taking $A = \operatorname{Eq}(f, g)$ and checking the identical morphism as FShrike said. And the original diagram is cartesian also following FShrike's answer.

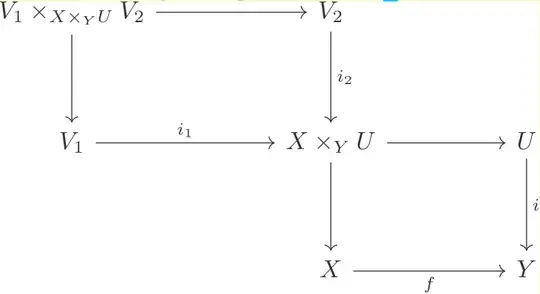
Despite checking the "to commute the limit operations and (co)yoneda applications" for the above specific case, it seems hard to make a general statement about it for the morphisms induced seems different from case to case, say $\operatorname{Eq}(f, g) \xrightarrow[]{\operatorname{can}} X$, or $\Gamma, \Delta$. For example for the third case in the question, it seems quite tedious to check $h(V_1 \times_{X \times_Y U} V_2) \cong h(V_1) \times_{h(X) \times_{h(Y)} h(U)} h(V_2)$ and the related diagrams are commute. Or for example the case shown up in Görtz&Wedhorn that involes a section is hard to include in some general concrete statement but requires specific handles.

Hence the idea here using the yoneda functor maybe treated as some guide line for some concrete proof after some conrete diagram shown up would be better.