Number of circular cylinders/cones through an ellipse

Question

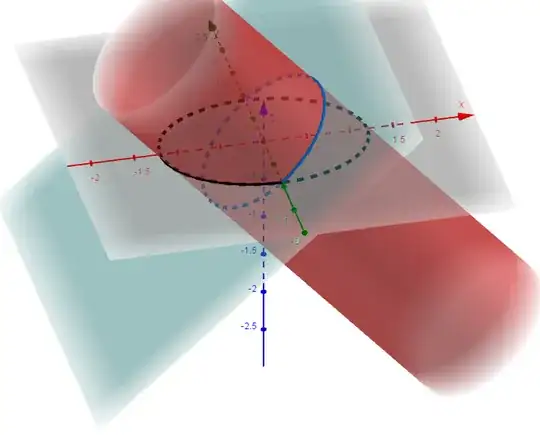
Given an ellipse $x^2 / a^2 + y^2 / b^2 = 1\;(a>b>0)$ on $xy$-plane.

Then an arbitrary elliptical cylinder through the ellipse has equation $(x / a + u z)^2 + (y / b + v z)^2 = 1$ for some $u,v\in\Bbb R$.

When does this equation represent a circular cylinder?

My attempt:

Expanding the left side of the equation: $x^2/a^2+2(u/a)xz+u^2z^2+y^2/b^2+2(v/b)yz+v^2z^2$.

the corresponding symmetric matrix is $$\left(\begin{array}{ccc} \frac{1}{a^2} & 0 & \frac{u}a \\ 0 & \frac{1}{b^2} & \frac{v}{b} \\ \frac{u}{a} & \frac{v}{b} & u^2+v^2 \end{array}\right)$$ The eigenvalues are (WA computation) \begin{align} \lambda_1= & 0 \\ \lambda_2= & \frac{1}{2 a^2 b^2}\left(a^2 b^2 u^2+a^2 b^2 v^2+a^2+b^2-\right. \\ & \left.\sqrt{\left(a^2b^2u^2+a^2 b^2 v^2+a^2+b^2\right)^2-4\left(a^4 b^2 u^2+a^2 b^4 v^2+a^2 b^2\right)}\right) \\ \lambda_3= & \frac{1}{2 a^2 b^2}\left(a^2 b^2 u^2+a^2 b^2 v^2+a^2+b^2+\right. \\ & \left.\sqrt{\left(a^2b^2u^2+a^2 b^2 v^2+a^2+b^2\right)^2-4\left(a^4 b^2 u^2+a^2 b^4 v^2+a^2 b^2\right)}\right) \end{align} Setting $\lambda_2=\lambda_3$ I get $$(a^2 b^2 u^2 + a^2 b^2 v^2+a^2 + b^2)^2 - 4 (a^4 b^2 u^2 + a^2 b^4 v^2+a^2 b^2)=0$$ Factorize (WA computation) $$0= (a^2 b^2 u^2 - 2 i a^2 b^2 u v - a^2 b^2 v^2 - a^2 + b^2) (a^2 b^2 u^2 + 2 i a^2 b^2 u v - a^2 b^2 v^2 - a^2 + b^2)$$ both real part and imaginary part must be zero, \begin{align} &a^2 b^2 u^2 - a^2 b^2 v^2 - a^2 + b^2=0\\ & u v=0 \end{align} If $u=0$, then $a^2b^2v^2=-a^2+b^2<0$, impossible.

If $v=0$, then $a^2b^2u^2=a^2-b^2$, I get $$u=\pm\frac{\sqrt{a^2-b^2}}{ab}$$

So $\lambda_2=\lambda_3=\frac{1}{b^2}$

The axis of the cylinder is $x/a+uz=y/b+vz=0$

The plane $-x u a - y v b + z = 0$ is perpendicular to the axis of the cylinder.

The section of the cylinder by the plane $-x u a - y v b + z = 0$ is a circle of radius $1/\sqrt{\lambda_2}=b$.

---

The above found there are only $2$ circular cylinders through a given ellipse.

Can we generalize the result to cones? (The cylinder case is the limit $\vartheta\to0$)

I guess:

Given an ellipse $x^2 / a^2 + y^2 / b^2 = 1\;(a>b>0)$ on $xy$-plane.
Given the opening angle $\vartheta\in(0,\pi)$ of the circular cone, there are only $4$ circular cones through the given ellipse.

The number is $4$ because reflections about $yz$-plane and $xy$-plane give different cones.

The $4$ cones will all be symmetric about $xz$-plane. Their vertices lie in each of $4$ quadrants of $xz$-plane.

Answer 1

From the properties of a planar cut through a circular cylinder of radius $r$ that makes an angle $\theta$ with its axis (i.e. the angle between the normal vector to the plane and the axis of the cylinder is $\theta$), we know that the cut will be an ellipse with semi-minor axis length of $r$ and semi-major axis length of $ \dfrac{r}{\cos(\theta) } $. Therefore, for the given ellipse, with $a \gt b \gt 0 $, it follows that $r = b $ and $ \theta = \cos^{-1} \left( \dfrac{b}{a} \right)$. The direction of this axis of this cylinder is either $N = (\sin(\theta), 0, \cos(\theta) ) $ or $N = ( - \sin(\theta), 0, \cos(\theta) ) $.

If $r = [x,y,z]^T $ then the equation of this circular cylinder is

$ r^T (I - {NN}^T ) r = b^2 $

Now, for $N = (\sin(\theta), 0, \cos(\theta) ) $,

$I - {NN}^T = \begin{bmatrix} \cos^2 \theta && 0 && -\cos \theta \sin \theta \\ 0 && 1 && 0 \\ - \cos \theta \sin \theta && 0 && \sin^2 \theta \end{bmatrix} $

Therefore, the equation of the cylinder is

$ \left( \dfrac{b}{a} \right)^2 x^2 + y^2 + (1 - \left(\dfrac{b}{a}\right)^2 ) z^2 - 2 \left( \dfrac{b \sqrt{a^2 - b^2}}{a^2} \right) x z = b^2 $

Note that if you substitute $z = 0$ you get the equation of the given ellipse.

A similar equation can be derived for the second value of $N$.

To summarize, there are two possible cylinders whose intersection with the $xy$ plane is the given ellipse.

For the circular cone, the reader is referred to this problem and its answer.