I was trying to solve this previous post by Mittens. I ended up having the answer for a different integral! And worse, Wolphram says it is $\approx 2,90179$, I found $3\pi/4\approx 2,356$. Anyways. Here is what I want to solve now:
Compute $$\int_{-\infty}^\infty \frac{dx}{\left(\frac89x^2+\frac23\right)\left({\frac{x^2}{3}+1}\right)^{3/4}}$$
We could approach this using complex analysis. Consider the following functions: $$f_1(z)=\frac{1}{\left(\frac89z^2+\frac23\right)e^{{\frac{1}{2}}\ln\left(\frac{z}{\sqrt{3}}-i\right)}}$$
$$ f_2(z)=\frac{1}{\left(\frac89z^2+\frac23\right)e^{{\frac{1}{2}}\ln\left(\frac{z}{\sqrt{3}}+i\right)}}$$
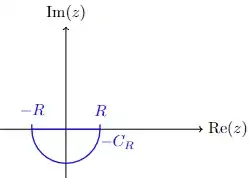
We notice that $\frac{z}{\sqrt{3}}-i=\frac{x}{\sqrt{3}}+i(y-1)$ which will always have an imaginary component in the following contour, so we are safe with the main branch of the logarithm regarding $f_1$:
By integrating $f_1$ there we see that on $C_R$:
$$ \left|\int_{C_R} f_1(z) dz\right|\leq \int_{-\pi}^0 \frac{R}{\left(\frac{8}{9}R^2-\frac{2}{3}\right)e^{\frac{1}{2}\ln(R)}}d\theta=\frac{\pi R}{\left(\frac{8}{9}R^2-\frac{2}{3}\right)\sqrt{R}}\xrightarrow{R\rightarrow \infty} 0$$
Furthermore, we have residues on $z^2=-\frac{3}{4}$, or equivalently, $z=\pm i \frac{\sqrt{3}}{2}$. Inside our contour, however, we need only compute:
$$\text{Res}_{z=-i\frac{\sqrt{3}}{2}}f_1(z)=\frac{1}{\frac{8}{9}\left(-2i\frac{\sqrt{3}}{2}\right)e^{\frac{1}{2}\ln(\frac{-i}{2}-i)}}=\frac{1}{\frac{-8i\sqrt{3}}{9}e^{\frac{1}{2}\left(\ln(\frac{3}{2})+i\frac{-\pi}{2}\right)}}=\frac{\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}}{\frac{-8i}{3\sqrt{2}}}$$
Hence, taking the limit (and observing that our contour is counterclockwise) yields:
$$-\int_{-\infty}^\infty f_1(x) dx=2\pi \frac{\sqrt{2}}{2}\frac{3\sqrt{2}}{-8}(1+i)=\frac{-3\pi}{4}(1+i)$$
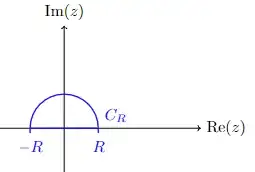
Similarly, taking the reflected contour with respect to the $x$ axis we may integrate $f_2(z)$, because it will be imaginary there and hence our branch logarithm will be well defined.
The integral over $C_r$ will vanish again and the residue will be
$$\text{Res}_{z=i\frac{\sqrt{3}}{2}}f_2(z)=\frac{1}{\frac{8}{9}\left(2i\frac{\sqrt{3}}{2}\right)e^{\frac{1}{2}\ln(\frac{i}{2}+i)}}=\frac{1}{\frac{8i\sqrt{3}}{9}e^{\frac{1}{2}\left(\ln(\frac{3}{2})+i\frac{\pi}{2}\right)}}=\frac{\frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2}}{\frac{8i}{3\sqrt{2}}}$$
Thus:
$$\int_{-\infty}^\infty f_2(z) dx=\frac{3\pi}{4}(1-i)$$
Of course, the logarithm is multiplicative in the range we are considering (one positive angle in $[0,\pi)$ and a negative angle in $(-\pi,0]$) from which it follows that:
$$\int_{-\infty}^{\infty}\frac{-e^{\frac{1}{2}\ln(\frac{x}{\sqrt{3}}-i)}+e^{\frac{1}{2}\ln(\frac{x}{\sqrt{3}}+i)}}{\left(\frac89x^2+\frac23\right)\sqrt{\frac{x^2}{3}+1}}dx=\int_{-\infty}^\infty f_1(z)-f_2(z) dx=\frac{3\pi i}{2}$$
Hence:
$$\int_{-\infty}^\infty \frac{2}{\left(\frac89x^2+\frac23\right)\left({\frac{x^2}{3}+1}\right)^{1/2-1/4+1/2}}dx=\int_{-\infty}^\infty \frac{-e^{\frac{1}{2}\ln(\sqrt{\frac{x^2}{3}+1)}}2\sin(Arg(\frac{x}{\sqrt{3}}-i)) }{\left(\frac89x^2+\frac23\right)\sqrt{\frac{x^2}{3}+1}} dx=\frac{3\pi }{2}$$
Finally (to our sadness):
$$\int_{-\infty}^\infty \frac{dx}{\left(\frac89x^2+\frac23\right)\left({\frac{x^2}{3}+1}\right)^{3/4}}=\frac{3\pi}{4}$$