Is every triangle a difference of two squares?

Question

Two complex numbers $z,w \in \mathbb C$ determine a triangle with the origin. The (signed) area of this triangle is $$A(z,w)=\frac{1}{2} \det \begin{pmatrix} \Re z & \Re w \newline \Im z & \Im w \end{pmatrix}.$$ You can verify that this is identical to the formula $A(z,w)=\frac 18 (|w+iz|^2-|w-iz|^2)$. This makes me think that there should be some kind of geometric construction that explains this identity, e.g. something like you can take a square in the plane (of some size and orientation), cut out another square, and then find that the leftover area decomposes into 8 identical triangles. I haven't been able to come up with such an argument or construction. And googling for things like "triangle area" or "triangle and difference of squares" only leads to things about high school geometry. Any thoughts?

Answer 1

This Geogebra applet () I made shows how to tile $[-B, B]^2 \backslash (-A, A)^2$, $B > A$, by $8$ congruent right triangles. And it's clear how to go from an arbitrary right triangle to a tiling of some $[-B, B]^2 \backslash (-A, A)^2$, $B > A$. By rotating the inside square by a specific amount, you can get a different tiling of a square-minus-square by congruent right triangles. More specifically, this is obtained by starting with a right triangle, reflecting the right-angle across the hypotenuse to obtain a kite, and then using four copies of this kite to produce the tiling of the square-minus-square. Here is a Geogebra applet (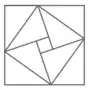) which shows this. The resulting algebraic identity from either construction is $(b + h)^2 - (b-h)^2 = 8 \cdot \frac{1}{2} bh$, where $b$ and $h$ are the lengths of the non-hypotenuse sides of the triangle. This exactly agrees with your version of the polarization identity when $z$ and $w$ are perpendicular.

You can do a similar construction for an arbitrary triangle by choosing one of its sides to be the base of a box and its height to be the height of the box. This splits a rectangle into two equal parts, and then you can tile the square-minus-square by four of these rectangles in the same way as before. However, the resulting identity $(b + h)^2 - (b - h)^2 = 8 \cdot \frac{1}{2} bh$ doesn't generally correspond to your polarization identity with respect to the vectors that determine the triangle.

Another way of viewing this last point is the following. Start with an arbitrary triangle. Note that a shear map is area preserving; this can be explained geometrically or algebraically. Shear map the triangle into a right triangle and compose it into either of the two constructions visualized above with Geogebra applets. This shows that the original triangle is one-eighth of the difference of squares. If you apply the inverse shear map to the first construction you'll get Daniel Schepler's construction.

Answer 2

Here's a somewhat involved geometric demonstration of the identity.

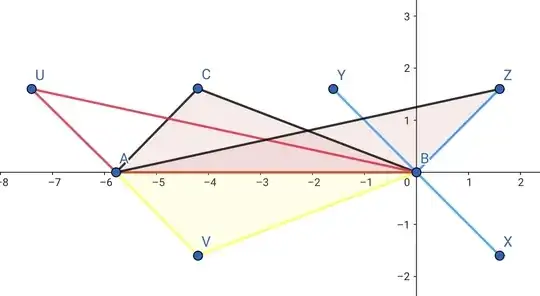
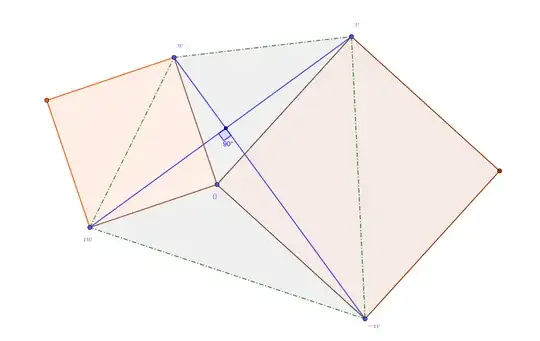
The first diagram below is an Argand diagram in which $\ w\ $ (here approximately $\ \frac{{-}33i}{8}\ $) and $\ z\ $ (here approximately $\ \frac{8}{5}(1+i)\ $) are represented by the points $\ A\ $ and $\ Z\ $ respectively. The points $\ Y,$$\,X,$$\,C,$$\,U\ $ and $\ V\ $ represent the points $\ iz,$$\ {-}iz,$$\,w+z,$$\,w+iz\ $ and $\ w-iz\ ,$ respectively. Thus, $\ YBX\ $ and $\ UAV\ $ are parallel straight line segments perpendicular to $\ BZ\ $ and twice its length, $\ AC\ $ is parallel to and the same length as $\ BZ\ ,$ the triangles $\ BAC\ $ and $\ BZA\ $ are congruent, $\ |BU|=|w+iz|\ ,$ and $\ |BV|=|w-iz|\ .$

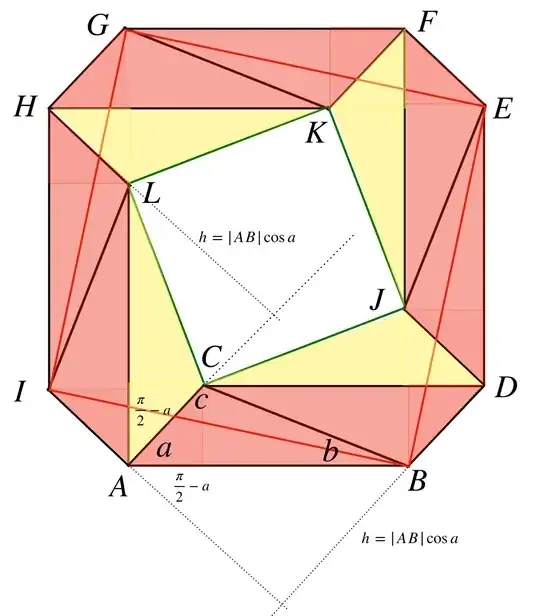
In the second diagram below, the eight red triangles are congruent to the triangles $\ ABC\ $ and $\ BZA\ $ of the Argand diagram, and the angles $\ BAL,$$\,CAI,$$\,IHK,$$\,LHG,$$\,GFJ,$$\,KFE,$$\,EDC\ $ and $\ JDB\ $ are right angles. As a consequence, the four yellow triangles $\ ACL,$$\,HLK,$$\,FKJ\ $ and $\ DJC\ $ are congruent to the triangle $\ ABV\ $ of the Argand diagram, the four triangles $\ IHG,$$\,GFE,$$\,EDB\ $ and $\ BAI\ $ are congruent to the triangle $\ BAU\ $ of the Argand diagram, the green quadrilateral $\ CJKL\ $ is a square with sides of length $\ |w-iz|\ ,$ and the red quadrilateral $\ IGEB\ $ is a square with sides of length $\ |w+iz|\ .$

Now \begin{align} \text{Area of square }\ IGEB=&\text{Area of octagon }\ BAIHGFED\\ &-(4\times\text{Area of triangle }\ BAI)\tag{1}\label{e1} \end{align} and \begin{align} \text{Area of square }\ CJKL=&\text{Area of octagon }\ BAIHGFED\\ &-(4\times\text{Area of triangle }\ ACL)\tag{2}\label{e2}\\ &-(8\times\text{Area of triangle }\ ABC)\ . \end{align} But the area $\ \frac{1}{2}|IA||AB|\cos a\ $ of triangle $\ BAI\ ,$ where $\ a\ $ is the size of the angle $\ BAC\ ,$ is the same as that of triangle $\ ACL\ $—namely $\ \frac{1}{2}|AC||AL|\cos a\ .$ Therefore, subtracting equation (\ref{e2}) from equation $(\ref{e1})$ gives \begin{align} 8\times\text{Area of triangle }\ ABC&=\text{Area of square }\ IGEB\\ &\hspace{2em}-\text{Area of square }\ CJKL\\ &=|w+iz|^2-|w-iz|^2 \end{align}

Answer 3

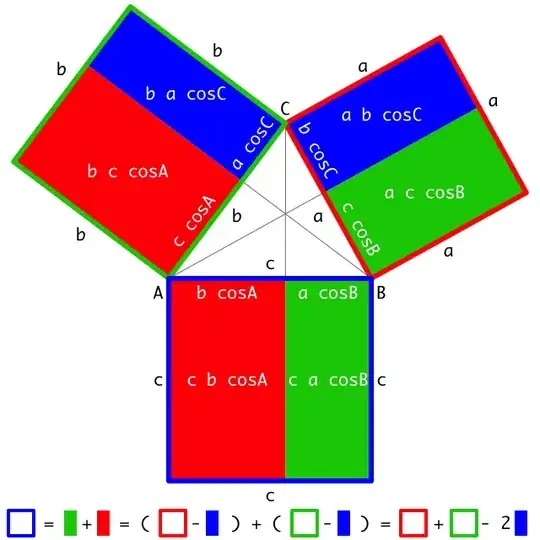
Here's a demonstration that leverages my diagrammatic proof of the Law of Cosines, a version of which is included at the end of this answer.

---

In detail ...

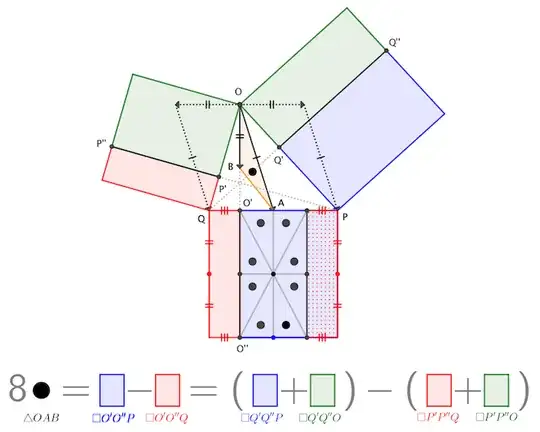
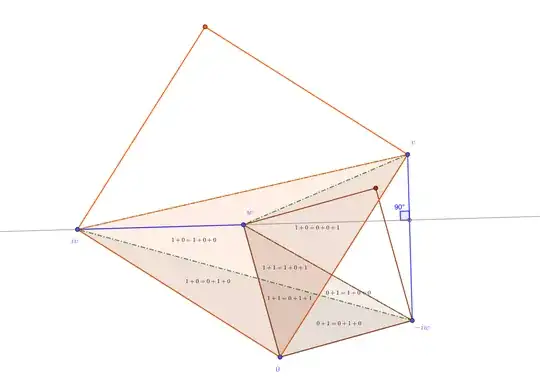
Take $O$ as the origin, and let $\overrightarrow{OA}$ and $\overrightarrow{OB}$ play the roles of complex numbers $w$ and $z$, so that $\overrightarrow{OP}$ and $\overrightarrow{OQ}$ represent $w+iz$ and $w-iz$.

On the sides of $\triangle OPQ$ —which we'll take as non-obtuse for this discussion— erect squares. Importantly, the lower square has side-length $2|OB|$, with $A$ the midpoint of one of the sides, and those sides are parallel and perpendicular to $\overline{OB}$ itself. Finally, drop perpendiculars from the vertices to give segments $O'O''$, $P'P''$, $Q'Q''$ that divide the squares into six rectangles that are pairwise equal in area. (Specifically, "green=green", "red=red", "blue=blue", which is the key observation in the Law of Cosines diagram.)

(BTW: To avoid cluttering the figure with vertex labels, I name each rectangle according to just three of its corners.)

We see that removing a copy of the lower red rectangle $\square O'O''Q$ from the lower blue rectangle $\square O'O''P$ leaves a centered rectangle that clearly sub-divides into eight equal triangles. Each triangle has a "base" (namely, $|OB|$) and corresponding "height" matching those of $\triangle OAB$; hence the areas match, as well. To complete the demonstration of the identity, we simply observe that "blue rectangle, minus red rectangle" is equivalent to "the square on $\overline{OP}$, minus the square on $\overline{OQ}$". $\square$

---

This approach is a bit less satisfying than, say, a explicit dissection of a difference-of-squares region into eight identical copies of the triangle. Here, except for slicing the central region into eight congruent pieces, the equalities of areas are effectively based on the invariance of area under shearing, which isn't always visually obvious. Nevertheless, the diagram seems to put the elements of the identity into a fairly natural configuration, and makes pretty clear how the factor of $8$ arises.

I should note: The Law of Cosines figure gets a little muddy for obtuse triangles. Everything still works (the Law of Cosines is always valid, after all), but needs to be slightly restated, typically in terms of "signed areas". Likewise, various relative positions of $\overrightarrow{OA}$ and $\overrightarrow{OB}$ complicate the figure above; accommodating those complications is left as an exercise to the reader.

---

For redundant reference, here's that proof of the Law of Cosines:

Answer 4

This is a good party, let me also join it, a lot of answers with interesting ideas. While trying to get the essence, and possibly simple pictures, i came to the following solution:

First picture:

We start with the grey triangle with vertices in $0,v,w$. Let $S=A(v,w)$ denote its area.

Squares are built on the two sides starting in zero. For each square the diagonal starting in $v$, respectively $w$ is drawn in green. These are two sides of a quadrilateral with perpendicular blue diagonals. Each diagonal has length $|w+iv|$. (Take the absolute value of the difference of the extremities. In the case with the difference $w-(-iv)$ things are clear. In the other case, $v-iw$, multiply with the modulus one complex number $i$.)

We compute the area of the quadrilateral delimited by the green segments in two ways.

• it is the sum of the gray equal areas, together with half areas of the squares.
• it is half the product of the diagonals. (Draw a square with the four vertices on the sides, with sides parallel to the blue diagonals.)

So this picture realized geometrically the identity: $$ S+S + \frac 12|v|^2 +\frac 12|w|^2 = \frac 12|w+iv|^2\color{gray}{=\frac 12|v-iw|^2}\ . $$

Second picture: The above gray part of the formula gives us a hint on how to obtain geometrically also the needed $\displaystyle \frac 12|w-iv|^2$ - we "only" need to exchange the places of $v$ and $w$. Doing so, we must recognize first where is the asymmetry in the above picture. It comes from building the orange square using an $i$-rotation ($+90^\circ$-rotation) of $w$, and a $-i$-rotation ($-90^\circ$-rotation) of $v$, so that the squares are drawn in the exterior of the triangle $(0,v,w)$. So let us draw the same picture "the other way around", the two squares will then point to the interior!

Also note that the signed area $S$ changes into $-S$, the orientation is changed.

In geogebra this is quickly done, we just destroy the above figure exchanging the places of the points $v,w$, and changing the labels to fit with the new positions. But why do we have the "same" formula in the new situation: $$ -S-S + \frac 12|w|^2 +\frac 12|v|^2 = \frac 12|w-iv|\ . $$ Working with negative areas is tricky, so let us work only with positive areas. We want to "see" the equivalent equality: $$ \frac 12|w|^2 +\frac 12|v|^2 = \frac 12|w-iv|+S+S\ . $$ In order to have a documented sight, inside each (colored) piece we have a parallel counting for it, corresponding to:

(orange half square) + (brown half square) = (quadrilateral) + (gray $\Delta(0,-iw,iv)$) + (gray $\Delta(0,v,w)$):

The quadrilateral piece is the non-convex area delimited by green segments. Again it is clear, that its area is the half the product of the two blue segments.

By isolating $2S$ from each formula and adding, we obtain: $$ 2S+2S=\frac 12|w+iv|^2-\frac 12|w-iv|^2\ . $$ $\square$

---

---

The brave reader may want now to put the two pictures over each other, and use for the first picture for the half squares the colors orange, and brown, for the second picture the colors minus orange and minus brown.

Answer 5

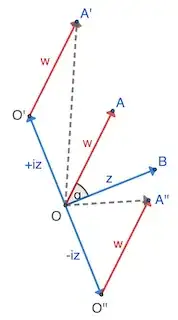
Slightly different from drawing squares, in the above visualization, $OA$ and $OB$ are $w$ and $z$, and $OO'$ and $OO''$ are $iz$ and $-iz$, respectively. Then $OA'$ is $w+iz$ and $OA''$ is $w-iz$. Note that $iz$ is a $90^o$ counter-clockwise rotation of $z$.

Writing the law of cosines for $\triangle{OO'A'}$ and $\triangle{OO''A''}$ we have: $$|OA'|^2 = |w+iz|^2 = |w|^2 + |z|^2 - 2|w||z|\cos(90^o+\alpha)$$ $$|OA''|^2 = |w-iz|^2 = |w|^2 + |z|^2 - 2|w||z|\cos(90^o-\alpha)$$ where $\alpha$ is the angle between $w$ and $z$. Then: $$|w+iz|^2 - |w-iz|^2 = 2|w||z|(\cos(90^o-\alpha)-\cos(90^o+\alpha)) = 4|w||z|\sin\alpha = 8S_{\triangle{OAB}}$$