$\DeclareMathOperator\li{li}$To derive the multivalued inverse of the logarithmic integral $y=\li(x)$$;y<0,x>1$, denoted $\li_-^{-1}(x)$ and for $0\le x<1$, denoted $\li_+^{-1}(x)$, we use:
We now invert $f(u)=\li(1\pm u)\implies f^{-1}=y$ using the derivative of an inverse function and substituting $u=\ln(v)+\gamma$ since $\li(1\pm u)\sim\ln(v)+\gamma$ with the Euler-Mascheroni constant $\gamma$:
$$(1\pm y)y’’(u)=y’(u)\iff\pm vy’’(v)=vy(v)y’’(v)+y(v)y’(v)$$
Now one has a differential equation for a solution to $e^{f-\gamma}=x$, plotted here from which one sees $y(0)=0,y’(0)=1$. Afterwards, we can set $\displaystyle y(v)=\sum_{n=1}^\infty a_nv^n$:
$$\pm v\sum_{n=1}^\infty n(n-1) v^{n-2}=v\sum_{m=1}^\infty a_m v^m\sum_{k=1}^\infty k (k-1) v^{k-2}+\sum_{m=1}^\infty a_m v^m\sum_{k=1}^\infty a_k kv^{k-1}\\\iff\pm\sum_{n=1}^\infty a_n n(n-1)v^{n-1}=\sum_{k=1}^\infty\sum_{m=1}^\infty a_ma_kk^2 v^{m+k-1}$$
equating coefficients with Kronecker delta, using its shifting property gives, and noticing $k$ goes up to $n-1$:
$$\pm a_n n(n-1)=\sum_{m=1}^\infty\sum_{k=1}^\infty a_m a_k k^2\delta_{n-1,m+k-1}\\\mathop\iff^{k=n-m}a_n=\pm\sum_{k=1}^{n-1}\frac{a_{n-k}a_kk^2}{n(n-1)}$$
Therefore we can rewrite to get:
$$\boxed{\li_\pm^{-1}(x)\mathop=^?1-\sum_{n=1}^\infty a_n (\pm1)^n e^{(x-\gamma)n}, n(n-1) a_n =\sum_{k=1}^{n-1}a_{n-k}a_kk^2=\left\{1,\frac12,\frac5{12},\frac{31}{72}, \frac{361}{720},\frac{4537}{7200},\frac{757517}{907200},\dots\right\}}$$
The series seems as correct plotting ContourPlot[{x== LogIntegral[y], y ==1-Sum[a[n] E^ ((x-EulerGamma) n), {n, 1, 13}],y==1-Sum[a[n] (-1)^n E^ ((x-EulerGamma) n), {n, 1, 13}]}, {x, -3,1}, {y, 0, 1.5}] with a[n] defined above:
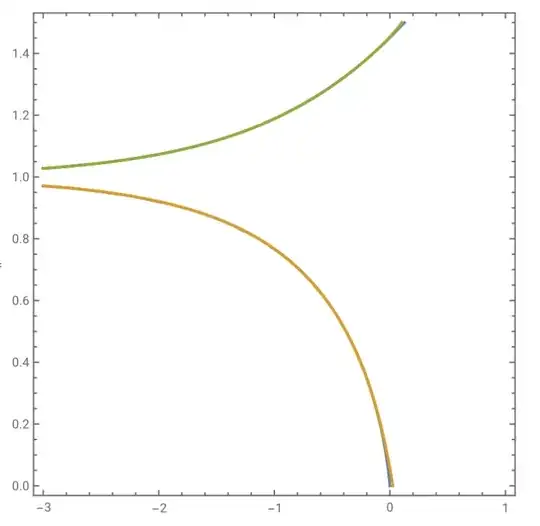
which implies the $\li_-^{-1}(x)$ series converges for $x<\mu$, the Ramanujan-Soldner constant and maybe $\displaystyle \mu=1-\sum_{n=1}^\infty a_n (-1)^n e^{-\gamma n}$. If the $\li^{-1}_+(x)$ series converges for all $x<0$, then the Golomb Dickman constant is $\displaystyle \lambda=1-\sum_{n=1}^\infty \frac{a_n e^{-\gamma n}}{n+1}$.
$a_n$ is likely correct as @Claude Leibovici found the same here.
Is there any way to simplify/rewrite it, like finding $a_n$ explicitly;