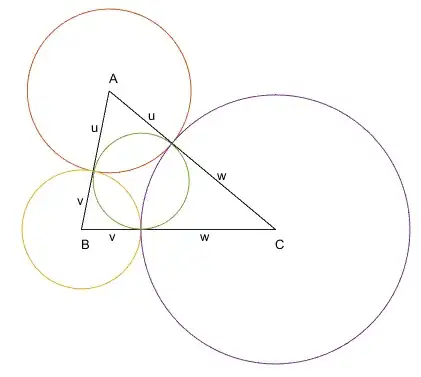The configuration space of 3 unordered points in $\mathbb{R}^2$ with distinct distances

Question

Let $(X, d)$ be a metric space and let $n \in \mathbb{N}$. Define $A_n(X) = \{ (x_i)_{i=1}^n \in X^n \mid \forall i \neq j: x_i \neq x_j \}$ to be the space of $n$ ordered distinct points in $X$. Define $B_n(X) = \{ (x_i)_{i=1}^n \in A_n(X) \mid \forall \{i, j\} \neq \{k, l\}: d(x_i, x_j) \neq d(x_k, x_l) \}$ to be the space of $n$ ordered distinct points in $X$ with distinct distances. Define $C_n(X) = B_n(X)/S_n$ to be the space of $n$ unordered distinct points in $X$ with distinct distances.

I'm trying to understand the space $C_n(X)$ in the smallest nontrivial case I could think of: $n = 3$ and $X = \mathbb{R}^2$. So, how can we describe $C_3(\mathbb{R}^2)$, the space of $3$ unordered distinct points in $\mathbb{R}^2$ with distinct distances, up to homeomorphism? What is its homotopy type?

Answer 1

The target of this answer is to provide a certain understanding of the "configuration space" of triangles with side lengths $(a,b,c)$ (with $a,b,c >0$) :

For any such triple $(a,b,c)$, there exists an alternative representation $(u,v,w)$, (with $u,v,w>0$) such that :

$$\begin{cases}a&=&&&v&+&w\\ b&=&u&&&+&w\\ c&=&u&+&v&&\\\end{cases}\tag{1}$$

with a geometrical interpretation of $u,v,w$) that can be seen on Fig. 1

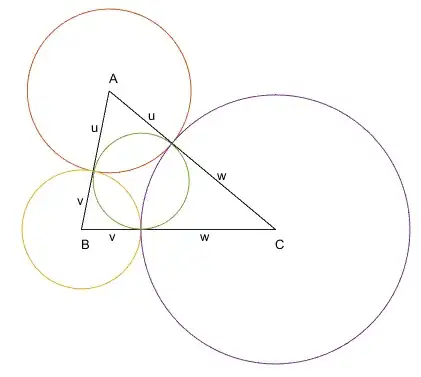
Fig.1 $u,v,w$ can be interpreted as the radii of mutually tangent circles centered in $A,B,C$ resp, all of them orthogonal to the incircle.

(1) can be written under the form :

$$\pmatrix{a\\b\\c}=\pmatrix{0&1&1\\1&0&1\\1&1&0} \pmatrix{u\\v\\w} \ \iff \ \pmatrix{u\\v\\w}=\tfrac12 \pmatrix{-1&1&1\\1&-1&1\\1&1&-1}\pmatrix{a\\b\\c} \tag{2}$$

As a consequence of (2), $u,v,w$ are positive due to triangle inequalities that can be written under the following form :

$$\begin{cases}(b+c)-a=2u > 0\\(c+a)-b=2v > 0\\(a+b)-c=2w > 0\end{cases}\tag{3}$$

Besides, (1) can be written in the following way :

$$\pmatrix{a\\b\\c}=u \pmatrix{0\\1\\1}+v \pmatrix{1\\0\\1}+w \pmatrix{1\\1\\0},\tag{4}$$

which means that the set of triangles can be represented wrt coordinates $a,b,c$ as

$$\text{the convex hull of half-lines} \ \ \mathbb{R}^+ \pmatrix{0\\1\\1}, \ \ \ \ \mathbb{R}^+ \pmatrix{1\\0\\1}, \ \ \ \ \mathbb{R}^+ \pmatrix{1\\1\\0}\tag{5}$$

---

Let us retrieve this result in a different manner.

Let us consider the Cayley-Menger determinant :

$$16\Delta ^{2}=\begin{vmatrix}0&1&1&1\\1&0&c^{2}&b^{2}\\1&c^{2}&0&a^{2}\\1&b^{2}&a^{2}&0\\\end{vmatrix} > 0 \tag{6}$$

where $\Delta$ is the area of the triangle.

In the present low-dimensional case, (6) is nothing else than Heron's formula

$$16 \Delta^2=(a+b+c)(b+c-a)(c+a-b)(a+b-c)\tag{7}$$

or, in terms of variables $u,v,w$, under the more compact form :

$$\Delta^2=(u+v+w)uvw\tag{8}$$

Expressing the positivity of product (7) is equivalent to say that the valid points are those already found in the first part : generic point $(a,b,c)$ must be on a certain side of three different planes, which amounts to say that it must belong to the non-bounded wedge-form volume whose truncation appears as a tetrahedron on Fig. 2.

Fig. 2.

Remark : the interest of Cayley-Menger expression is that it can be extended to any dimensions.

Answer 2

We may as well spend the $S_3$-action to identify $C_3(X)$ with the subset of triples $({\bf x}, {\bf y}, {\bf z}) \in B_3(X)$ for which $$d(y,z) < d(z, x) < d(x,y)$$ This approach is specific to $n = 3$, since for other $n$ there is no bijection between points and pairs of points.

Now specialize to $X = \Bbb R^m$, $m > 1$, in which setting the problem can be interpreted as asking for the configuration space of scalene triangles in $\Bbb R^m$. The translation $C_3(\Bbb R^m) \to C_3(\Bbb R^m)$, $$({\bf x}, {\bf y}, {\bf z}) \mapsto ({\bf x} - {\bf z}, {\bf y} - {\bf z}, {\bf 0})$$ translates each scalene triangle so that the vertex opposite its longest side sits at the origin. Since it preserves distances between components and, it yields a homeomorphism \begin{multline*} C_3(\Bbb R^m) \stackrel{\cong}{\to} \Bbb R^m \times \{({\bf x}', {\bf y}') \in (\Bbb R^m)^2 \mid ({\bf x}', {\bf y}', {\bf 0}) \in C_3(\Bbb R^m)\}), \\ ({\bf x}, {\bf y}, {\bf z}) \mapsto ({\bf z}, ({\bf x} - {\bf z}, {\bf y} - {\bf z})) . \end{multline*}

But the sides $\overline{{\bf 0}{\bf x}'}$ and $\overline{{\bf 0}{\bf y}'}$ of the translated triangle respectively have lengths $|{\bf x}'|$ and $|{\bf y}'|$, so the second factor of the above product is just $$\mathcal C := \{({\bf x}', {\bf y}') \in (\Bbb R^m)^2 \mid {\bf x}', {\bf y}' \in \Bbb R^m, |{\bf x}'| > |{\bf y}'|\},$$ which is the open cone of spacelike elements in $(\Bbb R^m)^2 \cong \Bbb R^{2 m}$ associated to the (indefinite) inner product (of signature $(m, m)$) characterized by $$||({\bf x}', {\bf y}')||^2 := |{\bf x}'|^2 - |{\bf y}'|^2 .$$ Via the map $({\bf x}', {\bf y}') \mapsto \left(\log ||({\bf x}', {\bf y}')|| , \frac{({\bf x}', {\bf y}')}{||({\bf x}', {\bf y}')||} \right)$ we can identify $\mathcal C \cong \Bbb R \times AdS_{m - 1, m}$, where the second factor is the anti-de Sitter space of signature $(m - 1, m)$, giving a homeomorphism $$C_3(\Bbb R^m) \cong \Bbb R^{m + 1} \times AdS_{m - 1, m} .$$

If the special case $m = 2$ (so, the configuration space of scalene triangles in the plane), $C \cong \Bbb R \times AdS_3$, where the second factor is $3$-dimensional (anti-)de Sitter space, which in turn is homeomorphic to $\Bbb R^2 \times \Bbb S^1$. So, concatenating our identifications yields a homeomorphism $$\boxed{C_3(\Bbb R^2) \cong \Bbb R^5 \times S^1} ,$$ which induces a homotopy equivalence $$\boxed{C_3(\Bbb R^2) \simeq S^1} ,$$ in agreement with Naïm Favier's conjecture in the comments..