Let $f(x) = \mu x(1-x)$ be the logistic map, the question is divided into 3 parts:
Part (1): what can you say about the domain of attraction of the 2-cycle in $3<\mu<1+\sqrt 6$?
My attempt: let $x_1, x_2$ be the 2-cycle, I know that $(f^2)'(x_1) = 4+2\mu-\mu^2$ and $3,1+\sqrt 6$ are roots to $4+2\mu-\mu^2 = \pm 1$ respectively, so for $3<\mu<1+\sqrt 6$, we have $|(f^2)'(x_{1,2})|<1$, so the 2-cycle is always stable. Then I can say the domain of attraction contains at least the neighbourhood of $x_{1,2}$, but can I derive a more concise interval that must be contained in the domain of attraction?
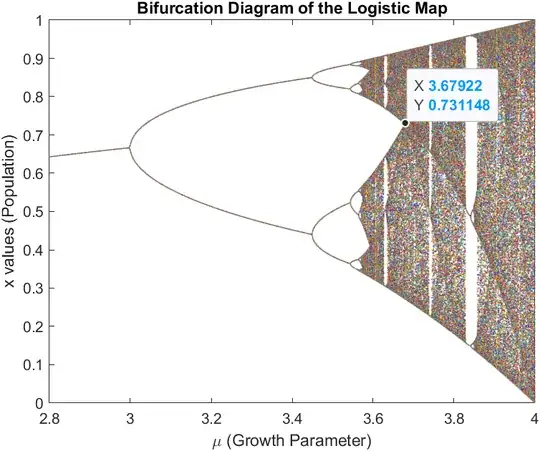
Part (2): in the bifurcation diagram for the logistic map there are several smooth dark tracks running through the chaotic part of the diagram. What are they? (hint: think about $f(\frac{1}{2},\mu)$).
My attempt: I think the dark track signify regions where the system's dynamics, despite being predominantly chaotic, organise into periodic orbits for certain parameter ranges. However, how will thinking about $f(\frac{1}{2},\mu)$ help me in this?
Part (3): these tracks all intersect at the tip of the white wedge at $\mu \approx 3.68$. can you obtain a more precise value of $\mu$?
My attempt: I need help on this question. I don't know where to start because I don't understand what this intersection at the tip of the white wedge could represent. Could someone help me out?
Any hint or full solution are greatly appreciated!