Probability of finding exactly one pair of cards: Almost perfect shuffles

Question

Consider a deck of 52 standard playing cards which contains cards of 13 different values (Ace, 2, 3,...10, Jack, Queen, King) in 4 different suits (shapes). The deck is thoroughly shuffled and spread face-up on a table so that all the values and suits are visible. The cards are spread along a line and not along a circle so cards in position 1 and 52 are not next to each other. What is the probability where exactly one pair of cards of the same value (any color) are located next to each other somewhere in the deck?

I was trying to solve this using Derangement, so first find the probability of having no pairs. This can be done by using PIE, since there will be 52 pairs of cards, $$D(52) = 52!-\ ^{52}C_1\ 2!\ (52-1)!\ + \ ^{52}C_2\ (2!)^2\ (52-2)! + ....$$ But I think I am undercounting the arrangements. Can someone help me with this?

Answer 1

The answer is given by

$$ \frac{13\cdot 4 \cdot 3}{52!} \int_0^\infty e^{-x}(x^{3} - 6 x^{2} + 6 x)(x^{4} - 12 x^{3} + 36 x^{2} - 24 x)^{12}dx = \frac{10971520051677934201049084030392994189}{75785709744934025854899427497123046875} = 0.144770301533151 $$

Notice: the integral turns $x^k$ into $k!$ and the calculation is thus trivial after multiplying out the polynomial inside. It's just notationally convienient.

Explanation: You pick what pair of cards is the adjacent pair and in which order it appears, hence the factor $13\cdot 4 \cdot 3$. Then you do the no pairs calculation for this modified deck where you assume that the pair you picked is glued together. I.e. you have only $3$ cards of the picked value and $4$ of the remaining $12$ values.

UPDATE: I made a Sage-function to calculate the probability that in a shuffled $k \times n$ deck ($k$ suits and $n$ values) there are exactly $r$ neighboring pairs of same value:

from collections import defaultdict, Counter
def getProb(k=4, n=13, r=1):
    R.<x> = QQ[]
    l = lambda m: sum((-1)jbinomial(m,j)binomial(m-1,j)factorial(j)x(m-j) for j in range(m+1))
    countNbrFree = lambda a: sum(c*factorial(j) for j,c in enumerate(prod(l(s) for s in a)))
def waysInsideOneValue(remParts):
    ret = 0
    for p in Partitions(k, length=remParts):
        w = 1
        rest = k
        for y in p:
            w *= falling_factorial(rest, y)
            rest -= y
        ret += w/prod(factorial(s) for s in Counter(p).values())
    return ret

wIVals = [waysInsideOneValue(j) for j in range(k+1)]

def genGluings():
    for c in Partitions(r+n, length=n, max_part=k):
        ways = multinomial(Counter(c).values())*prod(wIVals[k-y+1] for y in c)
        yield ways, tuple(k-y+1 for y in c)

ret = 0
for ways,a in genGluings():
    ret += ways*countNbrFree(a)
return ret / factorial(k*n)



myK = 4
myN = 13
ps = [getProb(myK, myN, r) for r in range(myK*myN-myN+1)]
eVal = sum(rp for r,p in enumerate(ps))
pFunc = lambda t: eVal(round(t))exp(-eVal)/factorial(round(t))
upR = 14
show(bar_chart(ps[:upR+1]).plot()+plot(pFunc, (0, upR), color='black'))

The Poisson approximation given in @Amir's solution is fairly accurate (drawn as a black curve):

UPDATE (24.5.2025):

It seems there's a better way to get the probability generating function:

def probGen(n, k):
    R.<x> = QQ[]
    N = k*n
    q = sum(binomial(k,j)*falling_factorial(k-1,j)*x^j for j in range(k+1))^n
    return list( sum(c/falling_factorial(N, j)*(x-1)^j for j,c in enumerate(q)) )

Answer 2

For each $i=1,\dots,13$, let us define $P_i(x,y)$ with $x\neq y\in S:=\{A,B,C,D\}$ as the event of that the card with number $i$ of suit $x$ appear just after the card with number $i$ of suit $y$. Then, the probability of having at least one pair is given by

$$P\left \{(\cup_{i=1}^{13}\cup_{x\neq y\in S}P_i(x,y)) \right\}, $$

which can be computed by the inclusion-exclusion principle considering that the probability of the intersection of any set of events $$P_i(x,y),i=1, \dots,13,x\neq y\in S,$$ can be obtained by counting, but different cases need to be considred. Note that the probability of having a perfect shuffle is

$$1-P\left \{(\cup_{i=1}^{13}\cup_{x\neq y\in S}P_i(x,y)) \right\}. $$

The probability of having exactly one pair in the shuffle (I call it almost perfect shuffle) can be computed using the following extension of the inclusion-exclusion principle:

If $(A_j)_{j\in J}$ is a finite or countable collection of events, then the probability that exactly $k$ of these events occur is $$p(k)=\sum_i (-1)^{i-k}{i\choose k}\sum \mathbb{P}\left(\bigcap_{j\in J(i)}\, A_j\right)$$ where the sum runs over all subsets $J(i)$ of the index set with $i$ elements.

Now the desired probability is obtained by applying the above to the events $P_i(x,y),i=1, \dots,13,x\neq y\in S$ for $k=1$.

For similar problems, see these old questions 2, 3, and 4.

Remark 1. The calculations are straightforward, but may take a long time. However, the exact formula can be used to calculate the probability with required accuracy. I mean using upper and lower bounds similar to Bonferroni-type inequlities, which require to calculate only a limited number of events.

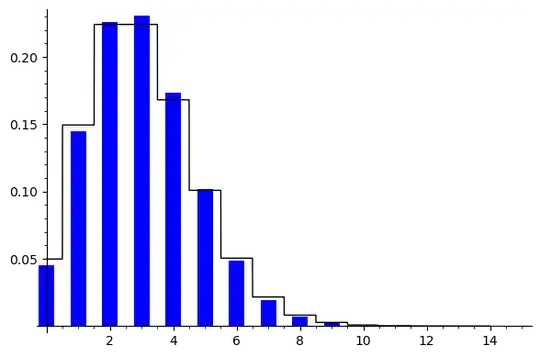
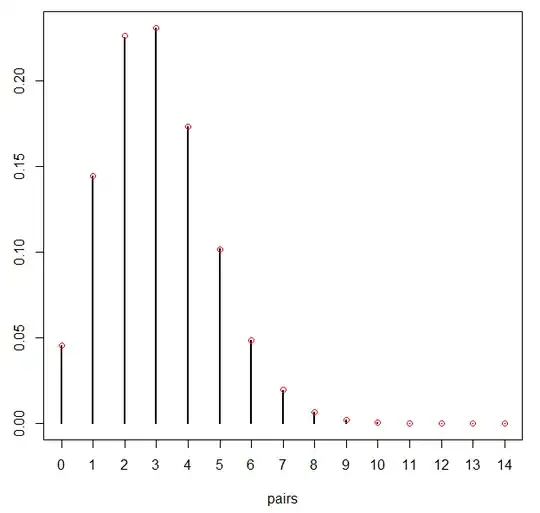
Remark 2. An approximate method to solve such a problem is to use Poisson approximation. We have $n=13×4×3$ events, each occurring with small probability of $p=\frac {1} {52}$, which are approximately independent; hence, the number of events that occur approximately follows Poisson distribution with $\lambda=n×p=3$. Thus, the probability of having an almost perfect shuffle is about $$P(X=1) \approx \frac{3^1e^{-3}}{1!}=0.149,$$ which is very close to the number $0.145$ obtained from stimulation by @paw88789. Also, it gives $$P(X=0) \approx \frac{3^0e^{-3}}{0!}=0.049,$$ which is very close to the probability of having a perfect shuffle obtained in 1 as $0.045$.

Answer 3

The purpose of this answer is to explain the background material cited in ploosu2's answer.

First, we set up the problem as Amir did in his answer. We are counting permutations of a set of $52$ cards while imposing several conditions, where each condition says that one particular card cannot follow another. Let $C$ be the set of conditions; explicitly, for each rank $r$, and each pair of distinct suits $s_1$ and $s_2$, there is a condition which says that $(s_1,r)$ cannot come immediately after $(s_2,r)$.

The generalized principle of inclusion exclusion says that $$ \text{# ways fulfill exactly one condition} = \sum_{S\subseteq C}(-1)^{|S|-1}\cdot |S|\cdot (\text{# ways fullfill conditions in $S$}) $$ Now, it turns out that you can prove the following:

Claim 1: For all $S\subseteq C$, the number of ways to fulfill all the conditions in $S$ is either $0$, or it is $(52-|S|)!$.

Proof sketch: First, consider when $|S|=1$. To be precise, say that the unique condition is that $\spadesuit2$ must come after $\newcommand{\sp}{\spadesuit} \sp 3$. When counting permutations that fulfill this condition, we can treat these two cards as a unit, and permute the entire sequence in $(52-1)!$ ways. When you have $k$ conditions, then there will be $k$ cards joined together like this, where each joining reduces the number of groups by $1$, so we permute the remaining $(52-k)$ groups in $(52-k)!$ ways. The exception is when the conditions are inconsistent; for example, if $S$ includes both "$\sp 2$ comes after $\sp 3$" and "$\sp 3$ comes after $\sp 2$", then all conditions in $S$ cannot be satisfied.

Let $c_k$ be the number of ways to choose a set of $k$ consistent conditions in $C$. With this definition, and using Claim 1, we can rewrite our previous equation as $$ \text{# ways fulfill exactly one condition} = \sum_{k=0}^{156}(-1)^{k-1}\cdot k\cdot c_k\cdot (52-k)! $$ All that remains is to compute the list of numbers $(c_0,c_1,\dots,c_{156})$. It turns out that there is a clever generating function solution.

Claim 2: $$\sum_{k\ge 0}^{156} c_kx^k=\left(1 + 12x+36x^2+24x^3\right)^{13}$$ Proof: Let us split up the process of choosing $k$ consistent conditions into two phases. In the first phase, we choose a list of number $(x_1,\dots,x_{13})$, where $x_i\ge 0$ for each $i$ and $x_1+\dots+x_{13}=k$. Then, in the second phase, for each $i\in \{1,\dots,13\}$, we will choose $x_i$ consistent conditions which involve the $i^\text{th}$ rank.

For each $j\in \{0,1,2,3\}$, let $r_j$ be the number of ways to choose $j$ consistent conditions in any particular rank. The number of ways to complete these two phases is $$ c_k=\sum_{x_1,\dots,x_{13}\ge 0,\\ x_1+\dots+x_{13}=k} \prod_{i=1}^{13}r_{x_i} $$ But this is just a $13$-fold Cauchy product of the series $(r_0,r_1,r_2,r_3)$. This implies the following generating function equation: $$ \sum_{k\ge 0}^{156} c_kx^k=\left(\sum_{i=0}^3r_ix^i\right)^{13} $$ Finally, you can prove that $$r_j=j!\cdot \binom{4}j\binom{3}j.$$ Indeed, there are $4\cdot 3$ ways to choose the first condition. Say we require that $\sp A$ comes after $\newcommand{\he}{\heartsuit}\he A$. Then we can treat the pair $(\he A,\sp A)$ as a unit, and count the number of ways to choose a condition among the three objects $(\he A,\sp A),\clubsuit A$ and $\diamondsuit A$. There are $3\cdot 2$ ways, to choose the next condition. In general, after $j-1$ conditions have been imposed, there are $(4-(j-1))\cdot (3-(j-1))$ ways to impose the next one, leading to $\frac{4!}{(4-j)!}\cdot \frac{3!}{(3-j)!}$ ways to impose $j$ conditions. However, we must divide by $j!$ to correct for the fact that order does not matter, leading to $\binom{4}{j}\cdot \binom{3}j\cdot j!$.

Answer 4

Essentially copied from an answer to a duplicate question

A binomial approximation is wrong, but easier than the exact calculation and closer than a Poisson approximation. The probability that a particular set of two cards have the same rank is $p=\frac{3}{51}=\frac{1}{17}$ so the expected number of pairs is $3$. With the false assumption these are independent, the probability of exactly one pair would be ${51\choose 1}p^1(1-p)^{50}\approx 0.14476858\ldots$

This compares to ploosu2's exact $0.14477030\ldots$ and Amir's Poisson approximation of $0.14936120\ldots$.

---

Simulation of the number of pairs (so with some simulation noise) suggests this may be quite good across the parts of the distribution with significant probability. Using R:

set.seed(2025)
suits <- 4
ranks <- 13
cards <- rep(1:ranks, suits)
cases <- 10^6
countpairs <- function(){ sum(diff(sample(cards)) == 0) }
pairs <- replicate(cases, countpairs())
mean(pairs) # should be about suits-1
# 3.001516
table(pairs)/cases
# pairs
#        0        1        2        3        4        5        6        7 
# 0.045523 0.144438 0.225555 0.231106 0.173531 0.102360 0.048600 0.019503 
#        8        9       10       11       12       13       14 
# 0.006728 0.001965 0.000542 0.000123 0.000017 0.000007 0.000002 

which, when compared to the suggested binomial approximation (red points), would look like

using

plot(table(pairs)/cases)
points(0:max(pairs), dbinom(0:max(pairs), suits*ranks - 1, 
                           (suits - 1) / (suits*ranks - 1)), col="red")