Suppose we have a set of points $x_1, \ldots, x_N$ in $R^d$ which we call the "bad set." Now we want an ellipse in $R^d$ of maximal volume, centered at point $c$, which does not contain any of the points in the bad set. See the image below, where the red dots are the bad set, and the blue ellipsoid is the sought ellipsoid.
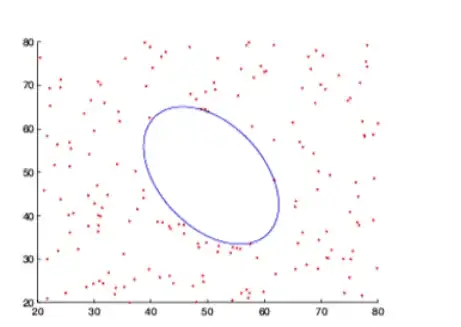
Figure 2.a from https://iopscience.iop.org/article/10.1088/1742-6596/1530/1/012087
Are there efficient algorithms known that solve this problem? There are similar problems for which quadratic programming solutions exist, e.g. the minimal volume ellipsoid containing a set of points (Löwner–John), and the maximum volume ellipsoid which lies inside a convex polyhedron. But the only solution I found for this particular problem are heuristic.
Heuristic algorithms
- Solution by genetic programming https://iopscience.iop.org/article/10.1088/1742-6596/1530/1/012087
- Solution by repeated reduction to the inscribed ellipse problem https://groups.csail.mit.edu/robotics-center/public_papers/Deits14.pdf