Determine the line equation on which the centers of all ellipse tangent to two lines at certain points lie

Question

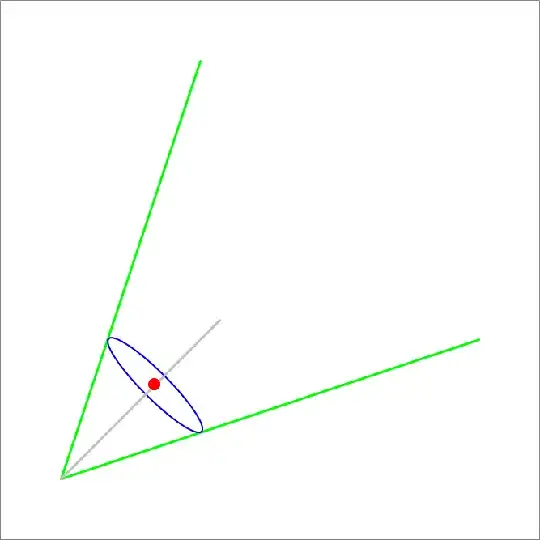
Given two lines, $\ell_1: y = 3 x - 2 $ and $\ell_2: y = \dfrac{1}{3} x + 6 $, and two points $P_1, P_2$ on lines $\ell_1$ and $\ell_2$ respectively, where $P_1 = (4, 10) $ and $P_2 = (6, 8) $, I want to find the equation of the line on which the center of all ellipses tangent to $\ell_1$ and $\ell_2$ at $P_1$ and $P_2$, respectively, lie.

What I've tried:

The equation of our ellipse is

$ (r - C)^T Q (r - C) = 1$

And the outward normal at a point $r_1$ is along the gradient of this quadratic function. That is,

$ k_1 g_1= Q (r_1 - C)$

For some $k_1$.

At $P_1$, the outward normal is

$ g_1 = \begin{bmatrix} -3 \\ 1 \end{bmatrix} $

And at $P_2$, the outward normal is

$ g_2 = \begin{bmatrix} \dfrac{1}{3} \\ -1 \end{bmatrix} $

Therefore,

$P_1 - C = k_1 Q^{-1} g_1 \hspace{10pt} (*)$

$P_2 - C = k_2 Q^{-1} g_2 $

I don't know how to proceed from this point.

Answer 1

I found the correct solution to my problem. It is the solution of @JeanMarie to a similar problem.

The trick to employ here is to create an affine transformation. The transformation relates two coordinate systems: Local given by $O'x'y'$ and world $Oxy$. In this case, the local coordinate system does not have its axes perpendicular to each other, and $Ox'$ and $Oy'$ have different scales.

Basically, we want to map the intersection point of our two given lines to the origin of the local frame $O'$, and we want the point $P_1(x_1,y_1)$ to map to $(1, 0)$ in the local frame, and the point $P_2 (x_2, y_2)$ to map to $(0, 1)$ in the local frame. This can be achieved as follows:

Let $(x_0 , y_0)$ be the intersection of the two given lines, then define the affine transformation as follows:

$ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x_0 \\ y_0 \end{bmatrix} + \begin{bmatrix} x_1 - x_0 && x_2 - x_0 \\ y_1 - y_0 && y_2 - y_0 \end{bmatrix} \begin{bmatrix} x' \\ y' \end{bmatrix} $

Now we want to work in the $O'x'y'$ plane, and our problem becomes finding ellipses that are tangent to the $x'$ axis at $(1, 0)$ and to the $y'$ axis at $(0, 1)$.

From the symmetry of the constraints, it follows (without proof), that the ellipse center must lie on the line $y' = x'$

Let $ x' = y' = \lambda $ , then the corresponding line in the world coordinates is

$ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x_0 + \lambda (x_1 + x_2 - 2 x_0) \\ y_0 + \lambda (y_1 + y_2 - 2 y_0 ) \end{bmatrix} $

And this is the equation of locus of the center of all ellipses satisfies the given constraints.