Given $a_1 < a_2 < ... < a_n$ and $f(x) = \sum_{i=1}^n |x - a_i|$, find a minimum
I had to look up the answer for this, and when I did, I still have some questions
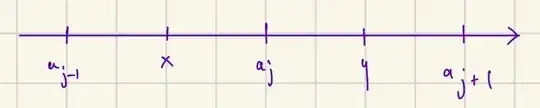
It starts off by considering some $x$ and $y$ that are equidistant from some $a_j$
1/ My first question is philosophical, and is in regards to why would one's thinking lead them to this approach when solving this problem. "I should consider what is happening to equidistant points around some $a_j$"
Next, they produce two equations:
If we consider some $a_i$ where $i \leq j - 1$, then we have
$$|y - a_i| = |x - a_i| + |y - x|, \space \forall i \leq j - 1$$
This makes sense
Now, we consider what happens for some $a_i$ where $i \geq j + 1$
2/ Now my second question concerns why we skipped over $j$. Provided I independently arrived at this step, I would not have thought to skip over an index.
$$|y - a_i| = |x - a_i| - |y - x|, \space \forall i \geq j + 1$$
The solution itself then goes on to say
$$f(y) = f(x) + |y - x| \cdot ((j - 1) - (n - j)) = f(x) + |y - x| \cdot (2j - n -1)$$
3/ How do we get this result
While I don't know how to answer my previous two questions, I attempted to answer this question. We must consider what happens to the function on three separate intervals: $[a_1, a_{j-1}]$, ??, $[a_{j+1}, a_n]$
$$ \begin{equation} \begin{aligned} f(y) = \sum_{i=1}^n |y - a_i| &= \sum_{i=1}^{j-1} \left(|x - a_i| + |y - x|\right) + \sum_{j+1}^n \left( |x - a_i| - |y -x| \right) + ?? \\ & = (j - 1)|y - x| + \sum_{i=1}^{j-1} |x - a_i| - (n-j)|y-x| + \sum_{i=j+1}^n |x - a_i| + ?? \\ & = f(x) + |y -x|(2j - n -1) \end{aligned} \end{equation} $$
And final question, which relates to question 1/
4/ How do we know that the two equations produced due to 1/ hold unique and distinct pieces of information about the original function that will yield fruitful result and not just cancel each other out. Because naively, you could argue that if you add those two equations together you get back a known result that $|y - a_i| = |x - a_i|$. If I independently arrived at those two equations, after having added them together and getting back this result, I would have likely not pursued this avenue further.