A probability involving areas in a random pentagram inscribed in a circle: Is it really just $\frac12$?

Question

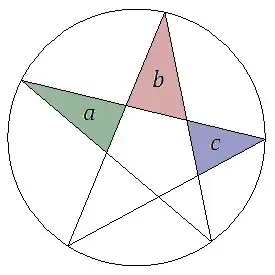
The vertices of a pentagram are five uniformly random points on a circle. The areas of three consecutive triangular "petals" are $a,b,c$. The petals are randomly chosen, but they must be consecutive, either clockwise or anticlockwise.

A simulation of $10^7$ such random pentagrams yielded a proportion of $0.5000179$ satisfying $a^2<bc$.

Is the following conjecture true: $P(a^2<bc)=\frac{1}{2}$

Remarks

Note that the three petals must be consecutive. Calling the areas of consecutive petals $a,b,c,d,e$, simulations suggest that:

• $P(a^2<bd)\approx0.468$
• $P(a^2<be)\approx0.505$
• $P(a^2<cd)\approx0.460$

Curiously, the probability that seems to equal $\frac{1}{2}$, i.e. $P(a^2<bc)$, does not involve a symmetrical arrangement of three petals.

As for other random star polygons $\{\frac{n}{2}\}$ inscribed in a circle, simulations suggest that

• Star polygon $\left\{\frac{6}{2}\right\}$: $P(a^2<bc)\approx0.505$.
• Star polygon $\{\frac{7}{2}\}$: $P(a^2<bc)\approx0.504$.

I used the shoelace formula to calculate the areas of the triangular petals.

One might expect that a probability of $\frac12$ should have an intuitive explanation, but sometimes probabilities of $\frac12$ are hard to explain.

Underlying reason?

Simulations suggest that the random pentagram/pentagon shape is teeming with probabilities of powers of $\frac12$. In the following diagram, the letters represent areas of the regions.

• $P(g+b+h<a+f+c)\overset{?}{=}\color{red}{\frac{1}{2}}$
• $P(g+h<f)\overset{?}{=}\color{red}{\frac{1}{4}}$
• $P((g+a+k)(h+c+i)>(b+f+e+d+j)^2)\overset{?}{=}\color{red}{\frac{1}{8}}$
• $P(\text{each region with area $g,b,f,l$ contains the centre of the circle})=\color{red}{\frac{1}{16}}$ (proved)
• $P(\text{areas of petals increase going around once, clockwise or anticlockwise})\overset{?}{=}\color{red}{\frac{1}{32}}$

I am not asking to prove these other probability claims. I am presenting them to suggest that there may be an underlying reason why the pentagram has probabilities of powers of $\frac12$, which may be relevant to my conjecture. These simulations make me more inclined to believe that my conjecture is true, but I could be wrong.

Answer 1

TL;DR: Simulation with larger sample-sizes effectively shows $P(a^2<bc)<{1\over 2}.$

EDIT: Although sample-size $10^{10}$ was adequate, I've updated to show the results for $10^{11}$.

For $p:=P(a^2<bc),$ your simulation with sample-size $n=10^7$ gave you an observed proportion $\hat p=0.5000179,$ so an approximate confidence interval with a $99.9\%$ "confidence level" is $$\hat p\pm 3.29\,\sqrt{\hat p(1-\hat p)\over n}=(0.4995, 0.5005).$$

Although ${1\over 2}$ does lie in this interval, the interval only estimates $p$ to about three digits of precision. Simulation using larger sample-size suggests -- with the same very high level of confidence/credibility -- that $p\ne {1\over 2},$ the difference showing up in the fourth decimal place. Here's a picture of what I find with sample-size $n=10^{11}$:

The posterior distribution is $\text{Beta}(a,b)$, with $(a,b)=(n\hat p+{1\over 2}, n(1-\hat p)+{1\over 2}),$ assuming a noninformative prior as $\text{Beta}({1\over 2},{1\over 2}).$ NB: With such a large sample size the posterior is insensitive to whether we use this prior or the flat Uniform prior, which is $\text{Beta}(1,1)$.

The $100(1-\alpha)\%$ credibility interval is therefore $$(B_{\alpha\over 2},B_{1-{\alpha\over 2}})$$ where $B_q$ is the $q$-th quantile of the $\text{Beta}(a,b)$ distribution.

The $100(1-\alpha)\%$ confidence interval is $$\hat p\pm z_{1-{\alpha\over 2}}\,\sqrt{\hat p(1-\hat p)\over n}$$ where $z_q$ is the $q$-th quantile of the standard normal distribution.

The sample-size of $10^{11}$ is sufficiently large that the various approaches to confidence/credibility intervals for $p$ should all give practically the same results (assuming a non-informative prior distribution in the Bayesian methods); e.g., they all give the same $99.9\%$ confidence/credibility interval for $p$, namely

$$0.499948 \pm 0.000005 = (0.499943, 0.499953).$$

---

EDIT: To perform a cross-check suggested in a comment, I re-ran the simulation with sample-size $10^{10}$, now using a completely different PRNG (Python's random.SystemRandom().random(), which is a much slower cryptographic PRNG). The resulting $99.9\%$ CI -- $0.49995 \pm 0.00002$ -- is consistent with the previous one for that sample-size -- $0.49994 \pm 0.00002$ -- and of course with the more-precise one given above for the $10^{11}$ sample-size.

---

Python code that I used for the simulation can be found here. It can also be run using the pypy interpreter for better speed; even so, on my system the simulation with sample-size $10^{11}$ took about 16 hrs.