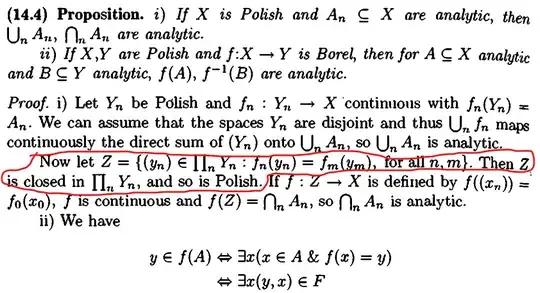I am trying to read Kechris book on Classical Descriptive Set Theory (self-studying only so please do bear with me). I need help in understanding the following part of the proof for (i) of Proposition 14.4.
From what I understand, a set $A$ is analytic if it is the projection of a closed set in $X \times \mathcal{N}$, where $X$ is Polish and $\mathcal{N}$ is the Baire space. However, $A$ by itself is not necessarily closed.
By a previous result, any Polish space $Y_n$ is homeomorphic with a closed subset of $\mathcal{N}$ - so we could suppose that $Y_n = \mathcal{N}$ for all $n$.
Now, in this proof, we have that $A_n = \{ f_n(x) : x \in \mathcal{N} \}$, so that $A_n$ is the projection of a closed set in $X \times \mathcal{N}$, i.e. the closed set $\{(f_n(x), x) : x \in \mathcal{N} \}$.
However, in this proof, we have that $Z$ is closed in $\Pi_nY_n$ (or in $\Pi_n \mathcal{N}$ if we take $Y_n = \mathcal{N}$ for all $n$) I don't follow why $Z$ is closed in this case. Any help ?