2

We want to find

$$I=\int_{-\pi}^\pi1+\lim_{n\to\infty}\min(\cos(x),\dots,\cos(nx))dx$$

Here is a picture of $1+\min(\cos(x),\dots,\cos(nx))$ for $n=50$:

$\displaystyle I_n= \int_{-\pi}^\pi1+\min(\cos(x),\dots,\cos(nx))dx$ has the following forms from software:

$$\begin{array}{r|c}I_1&2\pi\\\hline I_2&2\pi-3\sin\left(\frac\pi3\right)\\\hline I_3&2\pi-\frac13\left(9\sin\left(\frac\pi3\right)+5\sin\left(\frac\pi5\right)\right)\\\hline I_4&2\pi-\frac16\left(9\sin\left(\frac\pi3\right)+25\sin\left(\frac\pi5\right)+7\sin\left(\frac\pi7\right)\right)\\\hline I_5&2\pi-\frac1{30}\left(27\sin\left(\frac\pi3\right)+125\sin\left(\frac\pi5\right)+77\sin\left(\frac\pi7\right)+27\sin\left(\frac\pi9\right)\right)\\\hline I_6&2\pi-\frac1{30}\left(27\sin\left(\frac\pi3\right)+75\sin\left(\frac\pi5\right)+147\sin\left(\frac\pi7\right)+27 \sin\left(\frac\pi9\right)+22 \sin\left(\frac\pi{11}\right)\right)\end{array}\\\vdots$$

The denominators likely match A025555, the least common multiple of the first $n$ triangular numbers, so for $n>2$, we find:

$$I_n=2\pi-\frac2{\operatorname{LCM}(1,\dots,n)}\sum_{k=1}^{n-1}a_{n,k}\sin\left(\frac\pi{2k+1}\right)$$

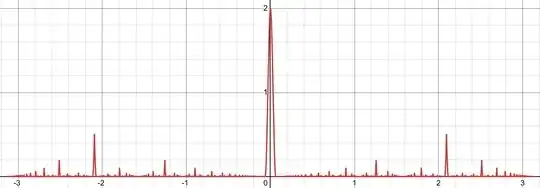
where the $a_{n,k}$ relates to A027446, “ Triangle read by rows: square of the lower triangular mean matrix”. Here is a graph showing the convergence as $n\to\infty$

$J=\int_{-\pi}^\pi1+\lim\limits_{n\to\infty}\min(\sin(x),\dots,\sin(nx))dx$ is also of interest. The fractals can be tested here. It seems that $\lim\limits _{n\to\infty}I_n=0$, but it is hard to tell.

How can one evaluate $I$, or maybe $J$?

Тyma Gaidash
  • 13,576
  • There is an easy way to evaluate it, but it really isn't rigorous –  Mar 29 '24 at 23:38
  • @Masd What do you mean it is not rigorous? – Тyma Gaidash Mar 29 '24 at 23:38
  • 1
    @TymaGaidash well there would be nuances that would be difficult to prove involving the fractal pattern, but perhaps it still would be easier to do than other methods –  Mar 29 '24 at 23:45
  • I'd say it converges to $0$, just try ramping it up to $5000$ elements, and it does make sense why –  Mar 29 '24 at 23:57
  • 1
    I think this question will be better if it was asked on MO – pie Mar 31 '24 at 07:03
  • What "fractal" do you see here? Can you precisely define the set which you are calling "fractal"? And what is your definition of "fractal" in that context? – Xander Henderson Apr 01 '24 at 23:00
  • @XanderHenderson Why ask these questions? You may see the Carotid-Kundalini Fractal and its reference. Also, $f(x)$ has detail when zoomed in at any scale, like the coastline fractal – Тyma Gaidash Apr 02 '24 at 00:32
  • @ТymaGaidash I ask the questions because my area of expertise is fractal geometry and analysis on fractals. The object you seem to have described does not meet any definition of "fractal" that I know, hence I don't know why you are calling it a fractal. But it is also possible that you mean some other object than the set you seem to have described. I also don't know what your link to the Carotid-Kundalini fractal has to do with this question. – Xander Henderson Apr 02 '24 at 00:54
  • As for "$f(x)$ has detail when zoomed in at any scale", that isn't a mathematically rigorous definition. The coastline paradox is a nice way of introducing someone unfamiliar with fractals to the idea of fractality, but it really only gives a rough first pass. It takes some work to build that up to real mathematics. – Xander Henderson Apr 02 '24 at 00:59
  • @XanderHenderson The Carotid fractal superimposes $\cos^{-1}(n x\cos^{-1}(x))$. $f(\cos^{-1}(x))$ here, superimposing $\cos^{-1}(n x\cos^{-1}(x))$ and minimizing is very similar. Maybe you can find its (noninteger) dimension, making it a fractal as seen here Also, $f(x)$ shows self similarity like in this plot. Maybe you can help via the above definitions/ references – Тyma Gaidash Apr 02 '24 at 01:55
  • 1
    Please do not use comments to complain about downvotes. It is not what comments are for. – Xander Henderson Apr 02 '24 at 01:59
  • Regarding the Carotid-Kundalini fractal, I don't see the connection to this question. – Xander Henderson Apr 02 '24 at 01:59

1 Answers1

4

For almost any choice of $x\in \mathbb{R}$, the set $$ \{\cos(nx) : n\in \mathbb{N} \}$$ is dense $[-1,1]$. Most books on ergodic theory likely have a proof of this fact, and it looks like there is already a proof on Math SE, so I will take this as given.

Note that $$ f(x) := 1+\lim_{n\to\infty} \min_{k\in\{1,2,\dotsc,n\}} \{ \cos(kx) \}. $$ Since $\{\cos(nx)\}$ is dense in $[-1,1]$ for almost every $x$, it follows that $f(x) = 0$ almost everywhere. To see this, note that if $x$ is such that $\{\cos(nx)\}$ is dense, then for any $\varepsilon > 0$, there is an $N$ such that $\cos(Nx) \in [-1,-1+\varepsilon)$. But then $$ f(x) = 1 + \cos(Nx) < 1 + (-1+\varepsilon) = \varepsilon. $$ This holds for any $\varepsilon > 0$, hence $f(x) = 0$ for any $x$ with $\{\cos(nx)\}$ dense (which is, again, almost every $x$).

If a function is zero almost everywhere, then it integrates to zero. Therefore $$ \int_{-\pi}^{\pi} f(x) \,\mathrm{d}x = \int_{-\pi}^\pi1+\lim\limits_{n\to\infty}\min(\cos(x),\dotsc,\cos(nx))\,\mathrm{d}x = 0.$$ A nearly identical argument applies to the other integral.

Xander Henderson
  • 32,453
  • This shows that the Lebesgue integral is zero. I suppose that the Riemann integrals is zero as well, though, that might be a bit trickier to prove. – Mark McClure Apr 05 '24 at 11:20