2

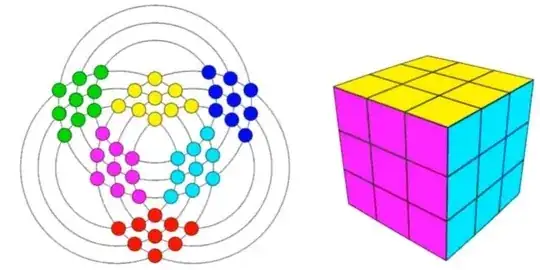
I'm a retired computer engineer and I'm studying a bit of abstract algebra these days.

I have done some research on the permutation groups of puzzles I've had a copy of the full partition of the 2x2x2 Rubik's cube for a while, and I think I can say it has an interesting structure, this partition.

It's embedded in $Z^2$, but really it has a 3 dimensional structure, you can roll up a section as a cylinder, so each section is a torus, and all the tori are nested. I figured out how to use the metric the authors used to count all the permutations, to embed the flat tori as a nested structure of open 'boxes' in $Z^3$.

I can demonstrate how this is all done with (what I think I've learned about) restriction and induction. I think the puzzles, along with a partition or part of one, are a good learning tool. Lots of ways to look at different things, apart from a color map.

But about the stochastic thing; this is about counting those permutations of a puzzle which are a pattern of some kind, and how to classify them. Does anyone have any background or hints?

Sigfreid
  • 29
  • Your question may look too broad for this site. This could draw downvotes and closevotes. Maybe it’s better make your question more specific. – Aig Mar 29 '24 at 22:53
  • It's hard for me to understand what is exactly your question. 1) What are the stochastic aspects you mention twice : where are the probabilities ? What do you mean by the terms "restriction" and "induction" ? When you mention "puzzles", which puzzles ? What is the meaning of the sentence "Lots of ways to look at different things, apart from a color map.". Etc. Sorry, but your question, in its present state is too allusive... – Jean Marie Mar 30 '24 at 00:47
  • There is an abundant litterature on Rubik's cube, in particular on this site. See for example here in a comment by Willie Wong an excellent Harvard reference. – Jean Marie Mar 30 '24 at 00:52
  • 1
    Afterthought : I understand now your question as "I have found something, I can present it to you, in order you say me what are your "feelings" about it and how I can go further. If it is so, please do insert the main "findings" of your research into this question ; I will surely react. – Jean Marie Mar 30 '24 at 10:12

1 Answers1

1

Are your "imbricated torii" more or less in connection with the following kind of "flattened representation" of the Rubik's cube ?

enter image description here

Jean Marie
  • 88,997
  • Extracted from this excellent youtube video – Jean Marie Mar 30 '24 at 17:15
  • ok. yes I think I have something and I want to see if I've done my homework. The partition of Perm{X} for the 2x2x2 cube is the output of a computer program. The table of numbers is a pattern, which informs me in some detail about how the group acts on {X}. Eventually I get to represent the action as a pair of loops on a single point. – Sigfreid Apr 01 '24 at 02:15
  • I can say for instance that the first section of Perm{X} as this table, is just the identity permutation and the generators-as-permutations, i.e. patterns, with the inclusion that each 4-cycle has a 2-cycle in it. The quarter-turn metric projects this to the point (1,2), the other two points in the table are (0,0) and (1,1). I can interpret this as notation for the number of 4-cycles on one or no faces. The point (1,2) is the 2-cycles on one face. – Sigfreid Apr 01 '24 at 02:22
  • How do you position your study with respect to questions like this one on Stack Exchange ? As there are a lot of studies about the $2 \times 2 \times 2$ Rubik's cube, gathering what has already been done and explaining you "added-value" would be beneficial for you and for your audience. 2) Could you produce for the $2 \times 2 \times 2$ cube a graphical representation similar to the one I have given in my "answer" ?
    • – Jean Marie Apr 01 '24 at 09:18
  • The GAP program in the answer to the question I was mentionning above can be executed in this (public domain) environment (select "GAP" instead of "SAGE") – Jean Marie Apr 01 '24 at 09:27
  • One thing about what i want to do is, it's the poset of all the permutations with a standard face coloring. It's a metric graph, and what I want to do is encode its structure, as if I'm designing say, a language or a computer of some kind. I've had some experience there, not as much as I'd like though. But a treatment as some formal language based on a string length, say. A grammar of some kind. The graphical representations of the cube-as-gadget, like the one posted are the local rep. I want the global one – Sigfreid Apr 01 '24 at 16:53
  • I do like that graph though. It looks easy to scale up or down, and it represents the orientations. – Sigfreid Apr 01 '24 at 16:57
  • The link in comment #1 has a bare or not-colored cube and then the author uses a "non-standard" coloring to represent the quaternions. That's nice. But . . . one quibble about both the bare cube (still a copy of S4) and rigid rotations. You have to switch from face to face, or otherwise allow for the change of coordinates in order to rotate part of the cube (1/2 in the illustration) at a time, it can't be done in parallel. The bare cube is colored, with 1 color. – Sigfreid Apr 01 '24 at 17:12
  • 1
    Um, what I should have said about that link is that it's one way to prove the quaternions exist in the group algebra. However it uses a particular graph coloring and the only metric is the pattern change. The patterns in the 3.7 million plus set with the standard face coloring are the pictures in the exhibition, but which ones have a regular, stochastic pattern? – Sigfreid Apr 01 '24 at 17:34
  • 1
    Just a comment about the graph on the left in Jean Marie's post. It's a planar graph with permutable colored points under rotation. But change the colors and the image of G acting on {X} changes. Say you color all the centres the same, etc. It's what is called a reduction, I believe. In this case the orbits of the centres would be reduced to 1. That means it's also a restriction on the centres – Sigfreid Apr 01 '24 at 21:00
  • I think it is valuable now to gather your detailed comments (in a structured manner) into your original question, explaining in detail the existing facts (such as the question/answer I have indicated), and what is the difference with what you want to obtain. – Jean Marie Apr 02 '24 at 11:21
  • 1
    About the quaternions being mapped to the 2x2x2 cube as in the animation. The quaternions can act together, since ijk = -1, this can't happen with a physical cube. Therefore the algebra in the cube rotations is iterated discretely. As Louis Kauffman explains, you need to characterize an iterant. The partition of Perm{X} is also iterated. So you can compose the quaternions on this discrete object, or with the cyclic graph or some other construction, but you can't get it to do parallel compositions. In other words, the map of Q8 is restricted, it has to be a composition of iterants. – Sigfreid Apr 02 '24 at 20:32
  • is a copy of that circular graph available? What does it let you do apart from rotations, or, is there a way to change the coloring? – Sigfreid Apr 02 '24 at 22:00
  • Which circular graph do you mean ? – Jean Marie Apr 02 '24 at 22:04
  • About what I'm trying to do at the moment. The partition has a first section, which I want to turn into a graphical representation of the group acting once on three centres of rotation. So it should map the identity permutation to the group action, on it and on itself, but in terms of iterating a 4-cycle. It doesn't matter how many times you iterate a group element on one centre, it only presents the permutations for that one centre. Then with this gadget I want to walk from section to section of the whole partition. – Sigfreid Apr 02 '24 at 22:05
  • the one in your post, next to the 3x3x3 cube with pink, yellow and blue faces. Is it available online? – Sigfreid Apr 02 '24 at 22:06
  • Yes in the Youtube video I mentionned just after my answer, where it is even animated ! – Jean Marie Apr 02 '24 at 22:18
  • 1
    Ok. I think I've managed to find out that it isn't an app. It's just an animation, but, it does underline that there are any number of ways to represent the action of the cube group. The vector space is just the group action as a function that permutes the basis, as long as you represent the basis correctly, you should recover Perm{X}, where {X} is the basis of distinguished points, say on the edge of a cylinder or something. That's how lecturers at Stanford explain it to grad students, at least. – Sigfreid Apr 02 '24 at 23:37
  • If I do post something of a treatise on this, it's going to cover a few bases in modern algebra. There is graph theory--the colored cube is a graph with colored faces--there is the fact that a chromatic polynomial applies to the cube before any analysis of the permutations is needed. The elements of the cube group are all cycles, composed of smaller cycles. The cyclic nature of the group means the partition can be explored piecewise by 'linear' cycles with odd or even order some are 5, some are 7 or 11 length cycles on the identity, but the orientations extend these, and there's a compaction – Sigfreid Apr 05 '24 at 03:38
  • I encourage you to do this under the form of an answer to your own question, ending (or beginning) by references to existing literature. It will be useful for many : the didactic way you propose here is very good. I will be happy to upvote it. – Jean Marie Apr 05 '24 at 08:33