Limit of lacunar power series in $1^-$.

Question

Let $\sigma:\mathbb{N}\longrightarrow\mathbb{N}$ be strictly increasing, and consider the power series $$ S_{\sigma}(x)=\sum_{n=0}^{+\infty}(-1)^nx^{\sigma(n)}. $$ Can any real number in $[0,1]$ be obtained as the limit $\lim\limits_{x\rightarrow 1^-}S_{\sigma}(x)$ for some $\sigma$ ?

According to this answer, the limit always is $\frac{1}{2}$ when $\sigma$ is a polynomial, WolframAlpha suggests that the limit is also $\frac{1}{2}$ with $\sigma(n)=n\log n$ (think of $\sigma(n)$ as the $n$-th prime number). Therefore my question can also be : Is the limit $\lim\limits_{x\rightarrow 1^-}S_{\sigma}(x)$ always $\frac{1}{2}$ ? if not, can any rational number in $[0,1]$ be obtained this way for some $\sigma$ ?

Answer 1

We show that if $\sigma(n)$ is exponential then the series tends towards $1/2$ but retains an oscillation about this value and does not completely converge.

Let $\sigma(n)=3^n$ and sum from $n=0$ to $n=\infty$, thus

$f(x)=\lim_{x\to1^-}\sum\limits_{n=0}^\infty (-1)^n x^{3^n}.$

The following graph shows a plot of this function from Microsoft Excel where data were obtained for

$x=1-3^{-k}$

with $k$ from $2$ to $12$ in increments of $1/4$ (we will see shortly why increments as large as $1$ would not work):

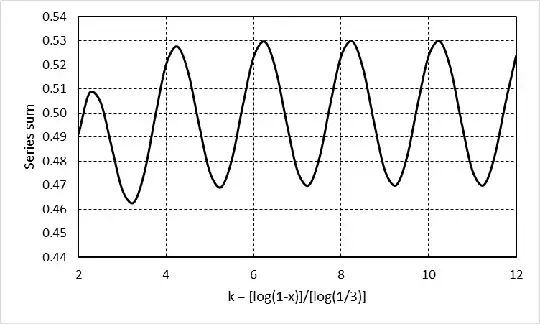
One might suppose the sinusoidal variation mught be due to roundoff error, but the operation is not particularly ill-conditioned and the $1-x$ values explored exceed $10^{-6}$ even at the right end of the graph (largest $k$, smallest $1-x$ explored).

What is really going on? Below is a graph showing how the absolute values of the summation terms decrease with increasing $n$ for various $k$ values.

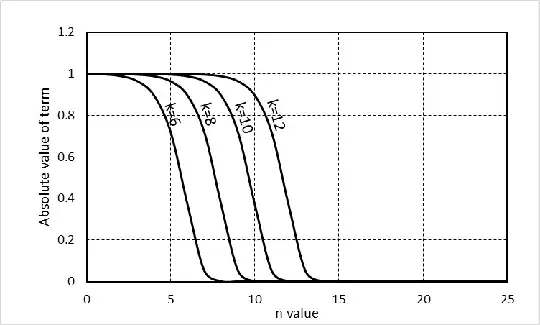
It becomes evident that the transition from $\pm1$ to $0$ in the terms tends to a constant shape that translates one unit towards increasing $n$ with each increment of one in $k$. This behavior would not be seen with a polynomial function for $\sigma$, for in that case the variation of $\sigma$ with $n$ would be slower and the transition would flatten out instead.

With the constant-shape transition comes a nonzero deviation from the limiting Cesarò sum of $\pm1$ terms, which modifies the $1/2$ that would be obtained from the $\pm1$ terms alone. We just saw that balancing an increment of one unit in $n$ with an equal increment of $k$ one unit preserves the absolute values of the respective terms in this region as $x\to1^-$, but the $n$ increment also changes the signs of the terms. Therefore each unit increment of $k$ will produce an undamped sign change in the curved region's contribution summed over all $n$. This oscillation characteristic matches the observed graph in the first figure above for $k>3, 26/27<x<1$.

Answer 2

My remark from MO ... $$\lim_{x \to 1^-}\sum_{k=0}^\infty \big(x^{10k}-x^{10k+3}\big) = \frac{3}{10} .$$ Similarly, get any rational in $(0,1)$.

Answer 3

Here is a full answer.

If $\frac{p}{q}\in(0,1)$, define $\sigma(2n)=nq$ and $\sigma(2n+1)=nq+p$, then $$ S_{\sigma}(x)=\sum_{n=0}^{+\infty}(x^{nq}-x^{nq+p})=\frac{1-x^p}{1-x^q}\underset{x\to 1^-}{\longrightarrow}\frac{p}{q} $$ as indicated by @GEdgar's answer. I'll prove that any $\alpha\in(0,1)$ can be obtained in the same fashion. Let $\sigma(2n)=n^2$ and $\sigma(2n+1)$ be the nearest integer of $n^2+\alpha(2n+1)$ in $(n^2,(n+1)^2)$, note that $\sigma$ is strictly increasing. Let $s=-\log x>0$, then $$ S_{\sigma}(x)=\sum_{n=0}^{+\infty}\int_{\sigma(2n)}^{\sigma(2n+1)}se^{-st}dt=s\int_0^{+\infty}\varphi'(t)e^{-st}dt $$ where $$ \varphi(t)=\int_0^t\sum_{n=0}^{+\infty}\mathbf{1}_{[\sigma(2n),\sigma(2n+1)]}(u)du. $$ An integration by parts gives $$ S_{\sigma}(x)=s^2\int_0^{+\infty}\varphi(t)e^{-st}dt+\mathcal{O}(s)=\int_0^{+\infty}s\varphi\left(\frac{u}{s}\right)e^{-u}du+\mathcal{O}(s) $$ with $u=st$. Let, for any $R>0$, $\Phi_R(u)=\frac{\varphi(Ru)}{R}e^{-u}$ so that $$ \int_0^{+\infty}s\varphi\left(\frac{u}{s}\right)e^{-u}du=\int_0^{+\infty}\Phi_{s^{-1}}(u)du $$ then $\Phi_R(u)\leqslant ue^{-u}\in L^1([0,+\infty))$. Let $N_R=\left\lfloor\frac{\sqrt{R}}{2}\right\rfloor$ so that $N_R^2\leqslant R\leqslant (N_R+1)^2$ then $$ \frac{1}{(N_R+1)^2}\sum_{n=0}^{N_R}(\sigma(2n+1)-n^2)\leqslant\Phi_R(1)\leqslant\frac{1}{N_R^2}\sum_{n=0}^{N_R+1}(\sigma(2n+1)-n^2). $$ But $|\sigma(2n+1)-n^2-\alpha(2n+1)|\leqslant\frac{1}{2}$ so $$ \frac{1}{(N_R+1)^2}\sum_{n=0}^{N_R}(\sigma(2n+1)-n^2)=\alpha+\mathcal{O}\left(\frac{1}{\sqrt{R}}\right)\underset{R\to+\infty}{\longrightarrow}\alpha $$ and the same goes for the RHS, therefore $\lim\limits_{R\to+\infty}\Phi_R(1)=\alpha$. But $\Phi_R(u)=u\Phi_{Ru}(1)\underset{R\to+\infty}{\longrightarrow}\alpha u$ for all $u>0$ thus $$ \lim\limits_{R\to+\infty}\int_0^{+\infty}\Phi_R(u)du=\int_0^{+\infty}\alpha ue^{-u}du=\alpha $$ by the dominated convergence theorem. The above computations allows us to conclude that $$ \lim\limits_{x\to 1^-}S_{\sigma}(x)=\alpha. $$

Answer 4

We obtain all possible rational limits by GEdgar's method. With a slight modification, it is possible to obtain any limit in $[0,1]$ in the following method.

Let $\alpha>1$. We consider $$ S_{\sigma}(x)=\sum_{n=0}^{\infty}(-1)^nx^{\sigma(n)}=\sum_{n=0}^{\infty} (x^{\lfloor \alpha n\rfloor}-x^{\lfloor \alpha n\rfloor+1})=(1-x)\sum_{n=0}^{\infty}x^{\lfloor \alpha n \rfloor}.$$ We define $\sigma(n)$ with the exponents in the powers of $x$ that are not cancelled out in $$ \sum_{n=0}^{\infty} (x^{\lfloor \alpha n\rfloor}-x^{\lfloor \alpha n\rfloor+1}). $$ Then the sum $S_{\sigma}(x)$ is Cesaro summable to $1/\alpha$. Thus, it is Abel summable to $1/\alpha$, yielding that $$ \lim_{x\rightarrow 1-} S_{\sigma}(x) = \frac1{\alpha}. $$

If we use $$ S_{\sigma}(x)=\sum_{n=0}^{\infty}(-1)^nx^{\sigma(n)}=(1-x)\sum_{n=0}^{\infty}x^{n^2} $$ so that the sum $S_{\sigma}(x)$ is Cesaro summable to $0$.

If we use $$ S_{\sigma}(x)=\sum_{n=0}^{\infty}(-1)^nx^{\sigma(n)}=(1-x)\left(\sum_{n=0}^{\infty} x^n -\sum_{n=0}^{\infty}x^{n^2}\right). $$ Then $S_{\sigma}(x)$ is Cesaro summable to $1$.