5

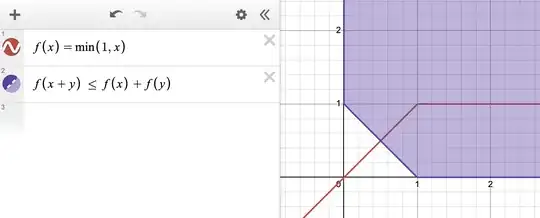
I was checking the subadditivity of the function $f\colon x\mapsto \min(1, x)$, i.e., whether $f(x + y)\le f(x) + f(y)$ and was expecting that the entire first quadrant would be colored. However, the following was outputted:

enter image description here

But clearly, for nonnegative $x, y$ satisfying $x + y < 1$, $f(x + y) \le f(x) + f(y)$ reduces to $x + y\le x + y$, which is true! So, what is Desmos doing here? (Interested in knowing "what went wrong" in Desmos' plotting alog's (of which I have no knowledge of, and would be delighted to be enlightened about!).)

To investigate, I also tried plotting $x + y\le x + y$ (or simply $x\le x$ for that matter), and Desmos showed no shaded region!

Edit

The correct plot should have been the first and the third quadrants translated by $(1, 1)$. It turns out that the region that Desmos has wrongly omitted to plot is precisely where the equality holds, that is, where $f(x + y) = f(x) + f(y)$, and as Kurt G. points out, this might be due to having x == y for floats x, y instead of demanding that abs(x - y) be smaller than a small positive precision. And indeed, plotting $|f(x + y) - f(x) - f(y)| < 0.0001$ gives the (approximate) remaining portion:

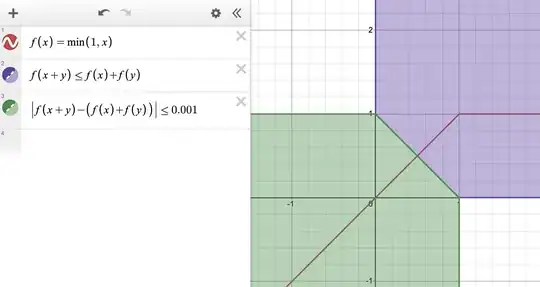
enter image description here

Atom
  • 4,620
  • It turns out that it must be the underlying plotting alog's, for snooping around some more, I found that adding a small constant (for instance, 0.000001) on the RHS does give reasonable results. But this shows that Desmos can't always be reliable. What checks do you guys use? – Atom Mar 18 '24 at 19:54
  • Common sense. No software is always reliable. +1 for finding this. – Kurt G. Mar 20 '24 at 05:21
  • @KurtG. Of course! But I am looking for "why". What causes the algo to fail? What is the plotting algo? – Atom Mar 20 '24 at 05:28
  • 1
    I am not the desmos programmer that should be asked. From professional experience I can tell you that it is quite common that programmers compare doubles in C++ with == which is a bad idea. Good programmers apply the trick you used and define equal(a,b) to be fabs(a-b) smaller than a small constant. It is pure speculation from an outsider if that or something similar is happening here. – Kurt G. Mar 20 '24 at 06:02
  • 1
    Perhaps it is: for any two $x,y$ in the region that desmos wrongly did not shade the two sides of the inequality are equal. To wrap this up for other readers can you post the correct plot also? That should be the first and third quadrant shifted by $(1,1),.$ – Kurt G. Mar 20 '24 at 06:07
  • @KurtG. Done. :) – Atom Mar 21 '24 at 00:06

0 Answers0