0

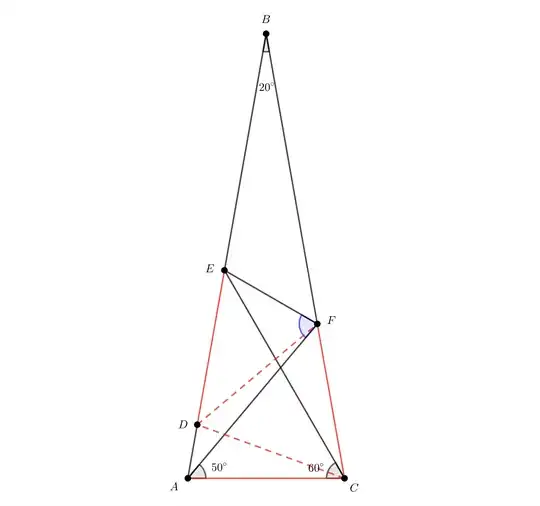
The problematic triangle in question

This problem with finding an unknown angle inside an isosceles triangle puzzled me for 5 years now.

My HS math teacher (who also taught at a local university) gave my class this problem in 2019 during my last year as a challenge. After a week without anyone finding an answer, we gave up. Now I'm almost done with my Masters in Data Science and I found it among my notes - I decided to make a nicer visualisation and try to find a solution. I also asked friends for help, but to no avail. One of my friends tried to calculate it using GeoGebra and got 80 degrees, but it is technically cheating...

Basically, the problem consists of an isosceles triangle with points labelled A, B, and C, with sides AB and BC being equal in length. Vertex B has a 20 degree angle. There are also a couple of internal triangles.

At point A, there is an angle of 50 degrees, and at point C, there is an angle of 60 degrees. One of the internal angles, adjacent to angle at point A, is labelled with an alpha, which is the angle we are asked to find. There are no other labels or numerical values provided. It was a while back, but from I can remember, my professor said the task required little more than "the basic principles of geometry".

Calculating the angle of the internal triangles at the bottom and on the sides is fairly simple, but finding the angles of the top triangle and the triangle containing alpha seems impossible - like there's not enough information, although perhaps there is some obscure rule that I wouldn't know how to apply.

All my friends couldn't manage to find a solution - hopefully one of you will be able to take a crack at it?

Jean Marie
  • 88,997
Kaellas
  • 3
  • This looks very familiar. I think this exact problem is at the end of Chapter 1 in Coxeter's Geometry Revisited. I won't spoil it but it doesn't need more than elementary techniques. – RobinSparrow Mar 12 '24 at 21:24
  • This is it! Thank you so much, this problem lived rent-free at the back of my head for years :) – Kaellas Mar 12 '24 at 22:26

1 Answers1

2

enter image description here

As @peterwhy have pointed out in the comments, this is a problem similar to Langley's Adventitious Angles. The key is to construct a equilateral triangle ($\triangle DFC$ in the figure above). Below is the solution to your problem.

Construct $D$ on $AB$ such that $\angle ACD=20^\circ$. From $\angle DAC=80^\circ$ we have $\angle ADC=80^\circ$, which implies $AC=DC$. Observe that

  • $\angle DCF=\angle ACF-\angle ACD=60^\circ$.
  • $AC=CF$ since $\angle CAF=\angle AFC=50^\circ$, and thus $AC=DC=CF$.

This means $\triangle DFC$ is an equilateral triangle. Now let's focus on $\triangle DCE$. We have $\angle ADC=80^\circ$ and $\angle DCE=60^\circ-\angle ACD=40^\circ$, which gives us $\angle DEC=40^\circ$. Therefore, $\triangle DCE$ is an isosceles triangle, and $DE=DC$. Hence $DE=DF$.

We're almost there. Note that $\angle DFA=\angle DFC-\angle AFC=10^\circ$, and $\angle DAF=30^\circ$. This implies $\angle ADF=140^\circ$, and thus $\angle DEF=\angle DFE=70^\circ$. Finally, $$\alpha=\angle EFA=\angle EFD+\angle DFA=70^\circ+10^\circ=80^\circ\,.$$

YanRuiJie
  • 56