I define the Fourier transform of a function $g$ to be $ \hat{g}(\lambda) = \int_{-\infty}^\infty g(x)e^{-i\lambda x} \, \mathrm{d}x $ with an associated inverse formula
$$ g(x)= \frac{1}{2\pi} \int_{-\infty}^\infty \hat{g}(\lambda) e^{-i\lambda x} \, \mathrm{d}\lambda. $$
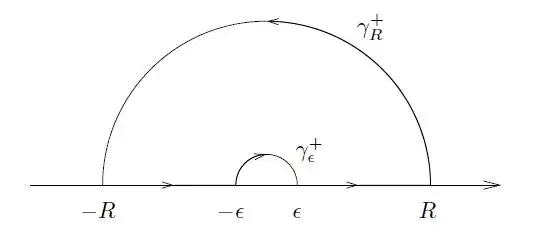
Fix $c>0$. I wish to verify this latter formula for the rectangular function $f(x) = \mathbf{1}_{|x| < \frac{c}{2}}$. Computing the Fourier transform is straightforward: after some manipulation, I find $ \hat{f}(\lambda) = \frac{2}{\lambda} \sin\left(\frac{\lambda c}{2} \right) $ so my task must involve evaluating $$ \int_{-\infty}^\infty \frac{2}{\lambda} \sin\left(\frac{\lambda c}{2} \right ) e^{i\lambda x}\, \mathrm{d}\lambda. $$ It seems like I can do this using contour integration. It seems like I should be using the following contour (image taken from this question):
and sending $\epsilon \to 0$ and $R \to \infty$ to evaluate the integral. But I'm not sure how I should handle the boundary terms: for instance, parametrising the outer semicircle as $\gamma(t) = Re^{i \pi t}$ for $t\in [0,1]$ leaves the contribution $$ \lim_{R \to \infty} \int_0^1 \frac{2}{Re^{i \pi t}} \sin\left( \frac{cRe^{i\pi t}}{2} \right) e^{ix Re^{i\pi t}} \cdot \left( Ri\pi e^{i\pi t} \right) \, \mathrm{d}t = 2\pi i \lim_{R \to \infty} \int_0^1 \sin\left( \frac{cRe^{i\pi t}}{2} \right) e^{ix Re^{i\pi t}} \, \mathrm{d}t $$ which seems intractable, even after assuming I can pass the limit through the integral. Even if I can find the resulting value, it's not clear to me where the dependence on $c$ arises, since we want to attain $1$ if $|x|<c/2$ and $0$ otherwise. Am I missing something obvious?