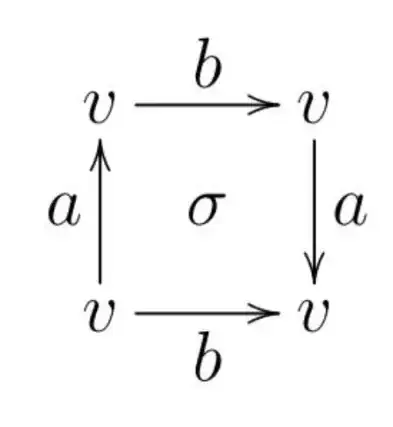
Homology groups of the Klein bottle

Question

I've seen this but didn't really understand the answer. So here is what I tried:

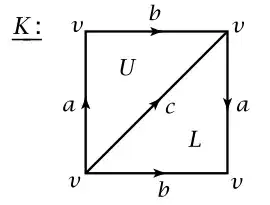
enter image description here

According to this picture we have one 0-simplex - $[v]$, two 1-simplices - $[v,v]_a,[v,v]_b$ and two 2-simplices - $[v,v,v]_U,[v,v,v]_L$.

The chain complexes

$C_0=\{nv:n\in\Bbb{Z}\}, C_1=\{n[v,v]_a+m[v,v]_b+k[v,v]_c:n,m,k\in\Bbb{Z}\}, C_2=\{n[v,v,v]_U+m[v,v,v]_L:n,m\in\Bbb{Z}\}$.

Boundary maps

$∂_0=0, ∂_1([v,v]_a)=[v]-[v]=0$,

$∂_2([v,v,v]_U)=[v,v]_a+[v,v]_b-[v,v]_c=[v,v]_a$ and $∂_2([v,v,v]_L)=[v,v]_a-[v,v]_b+[v,v]_c=[v,v]_a$.

I think $\operatorname{Im}∂_2$ is the set of multiples of $[v,v]$ which is isomorphic to $\Bbb{Z}$ but I'm not sure about this. Once I know $\operatorname{Im}∂_2$ it's easy to calculate $\ker{∂_1}/\operatorname{Im}∂_2=H_1(K)$ as $\ker{∂_1}=\Bbb{Z}^3$.

Could you explain what is $\operatorname{Im}∂_2$?

Ted Shifrin · Accepted Answer · 2013-09-08T11:49:23.693

6

You obviously have a typo, having forgotten to include the $1$-simplex $c$. Your "simplifications" of $\partial_2$ are incorrect. To save typing, I'll write $\partial_2 U = a+b-c$ and $\partial_2 L= a-b+c$. If you make the change of basis (over $\mathbb Z$) $a'=a+b-c$, $b'=b-c$, $c'=c$, you can easily check that $a', a'-2b'$ give a basis for $\text{im}\,\partial_2$. So $H_1 \cong \mathbb Z\oplus \mathbb Z/2$.

edited Sep 08 '13 at 11:49

answered Sep 08 '13 at 11:41

Ted Shifrin

125,228

Why are my simplifications of $\partial_2$ incorrect? – Xena Sep 08 '13 at 11:47
Because the three $1$-simplices $a$, $b$, and $c$ are all independent — they're the generators of $C_1\cong\mathbb Z^3$. – Ted Shifrin Sep 08 '13 at 11:48

score 2 · Answer 2 · edited Mar 09 '17 at 17:30

It seems it is a long way from being accepted that to write the boundary of the diagram

klein

we need write only the nonabelian formula (assuming base point the top left corner)

$$\delta \sigma= b +a -b +a $$

saving all that decomposition into simplices. For more information see my presentation at Chicago, 2012. It is also true that it does require new ideas to make a complete story, like crossed modules, free crossed modules ($\sigma$ is a generator of a free crossed module, and $a,b$ generate a free group), and the complete story is in the book "Nonabelian algebraic topology", 2011, EMS Tract 15. Other presentations (2014, 2015) are on my preprint page (Galway, Aveiro, Liverpool,...). All this stems from and develops the work of J.H.C. Whitehead in his paper "Combinatorial Homotopy II".

Homology groups of the Klein bottle

2 Answers2

Linked