1

Though this question doesn't have mathematical origins, it boils down to geometry. I'm a high school student so forgive me if the answer is obvious, I will likely have overlooked it.

I am building a robot which is controlled like a tank, with one set of wheels on each side being controlled by a driver, allowing me to power each side of the robot individually, causing the motion of the robot when rotating to essentially be an arc. The sensors retrieve enough data to know the orientation of the robot, its position and the position of the destination. The algorithm itself is part of the robot's course correction, and must bring the robot to the destination, leaving it facing north.

To reduce the sharpness of the turns as much as possible whilst maintaining simplicity, I've decided to to model the path of the robot as two arcs of equal radius. I want to know the position or bearing of the robot when it has to change arcs in terms of the data available to me. I know each set of data has one unique solution, and I've already tried my hand at writing an equation which is as follows: $$ 2wsin(\theta)−2hcos(\theta)=hcos(\phi)+h−wsin(\phi) $$ with $h$ being the vertical distance between the points, $w$ being the horizontal displacement and $\phi$ being the initial bearing of the robot.

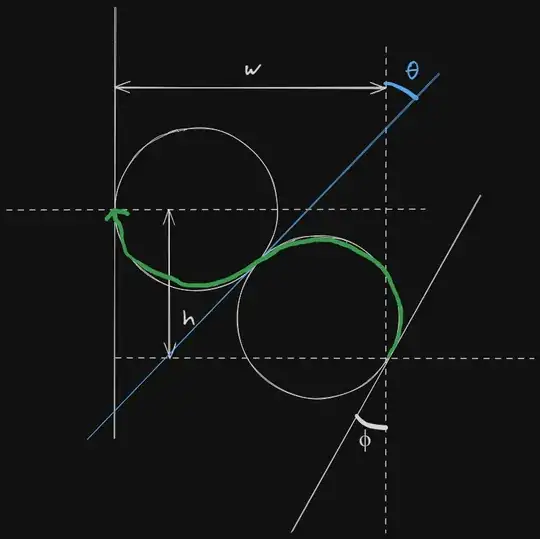
Below is a diagram of the problem enter image description here

However, I don't know how to solve this equation and I don't know if any simplifications exist. Bear in mind that this is a narrow-face part of a course correction algorithm, so values of $w$ and $\phi$ will be small, and efficiency is just as, if not more, important than accuracy, so heuristics are more than welcome, as are modifications to the model. I'm treating the solution like a formula at the moment but it's an algorithm, so the problem is extremely flexible.

Thanks for your help.

user17301834
  • 123
  • What is $\theta$ in your equation? – Intelligenti pauca Feb 27 '24 at 20:24
  • I'll add $\theta$ to the diagram but its essentially the angle between the front of the robot and the normal when it moves from one arc to the other, or at the intersection of the two circles – user17301834 Feb 27 '24 at 20:25
  • The green line is the path of the robot – user17301834 Feb 27 '24 at 20:29
  • How did you get that equation? And why doesn't it involve the radius of the circles? – Intelligenti pauca Feb 27 '24 at 20:35
  • I got the equation by considering the radii of the circles and the lines connecting the points to the centres of each circle before taking the vertical and horizontal components of the lines when drawn together and solving simultaneously to cancel out $r$. I don't know whether or not my equation is correct but I don't see any flaws in my working – user17301834 Feb 27 '24 at 20:40
  • Basically I drew lines connecting the points to the centres of their corresponding circles and a line connecting the two centres, then treating each line somewhat like a vector. Considering the horizontal component of the sum of the lines gives the equation $r(1+cos(\phi)+2cos(\theta))=w$ and the horizontal component gives $r(sin(\phi)+sin(\theta))=h$. – user17301834 Feb 27 '24 at 20:44
  • I see: I've just made the same reasoning and can confirm your equation is correct. – Intelligenti pauca Feb 27 '24 at 20:44
  • Thanks, if you can't find an efficient solution a heuristic or alteration to the problem would be much appreciated but its no problem – user17301834 Feb 27 '24 at 20:45
  • 1
    A standard way to solve that equation involves the substitutions: $$\sin\theta={2t\over1+t^2},\quad \cos\theta={1-t^2\over1+t^2},\quad \text{where}\quad t=\tan{\theta\over2}.$$ You get a quadratic equation in $t$ which is easy to solve. – Intelligenti pauca Feb 27 '24 at 20:48
  • Thanks, this is exactly what I was hoping for when posting this question. I'll leave it open just in case a heuristic exists because I'm starting to worry about the efficiency of the algorithm but your help is appreciated! – user17301834 Feb 27 '24 at 22:14

1 Answers1

0

The problem can be solved using addition formulae to give the formula: $$ \theta = \arccos\left(\frac{h\cos(\phi)+h−w\sin(\phi)}{2\sqrt{h^2+w^2}}\right)+\arccos\left(\frac{-h}{2\sqrt{h^2+w^2}}\right) $$

TShiong
  • 1,270
user17301834
  • 123