Unit circle trigonometric functions are defined on the graph $x^2+y^2=1$. Hyperbolic trigonometric functions are defined on the hyperbola $x^2-y^2=1$.
If I would want to define other trigonometric functions on a completely different graph,
a) What properties would be useful to preserve? I'm not an expert on trigonometry, but after watching a few videos on the topic, I know hyperbolic trigonometry keeps the area with the point $(\cosh a, \sinh a)$ between the graph to be $\frac{1}{2}a$. Are there any other relationships that would want to be preserved?
b) Would the graph $\pm x^{\frac{1}{2}}$ work? What would the respective trigonometric functions be? Could they be expressed in already-known trigonometric functions? If so, is there a completely new graph with its functions?
This might be a completely dumb question, but I'm just curious about why trigonometry is limited to a hyperbola and circle. There are relations with $e$ and even-odd functions, but is there anything else?
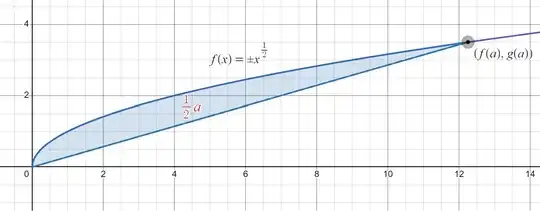 $\pm x^{\frac{1}{2}}$" />
$\pm x^{\frac{1}{2}}$" />