Why is $AA^TAA^TAA^TAA^T$ larger than $AAAAA^TA^TA^TA^T$ for Gaussian $A$?

Question

Suppose $A$ is a $d\times d$ matrix with IID standard normal entries.

Plots below compare value of $f(AA^TAA^TAA^TAA^T)$ and $f(AAAAA^TA^TA^TA^T)$ using 3 standard Schatten norms for $f$ and the former is consistently larger, why?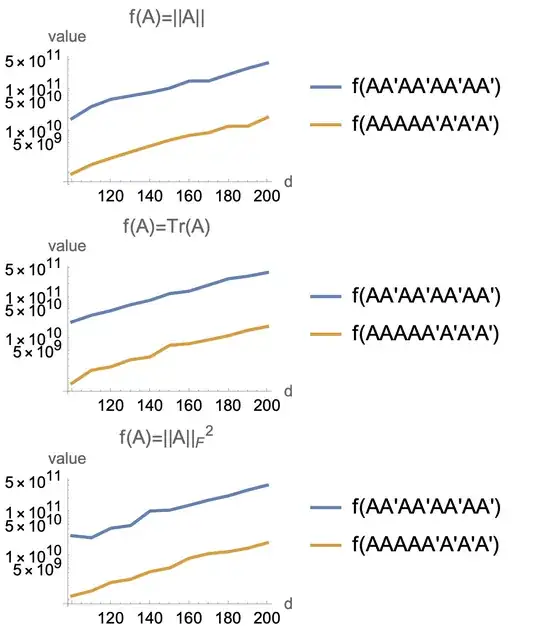

Furthermore, we can compute expected values of $Tr(A\ldots)$ for $d=2$ and various permutations of $A$, and these two forms appear to be the extreme values. What's the easiest way to explain this?

getVal[d_, f_, sampler_] := (
   A = sampler[d];
   {Norm[
     A . A\[Transpose] . A . A\[Transpose] . A . A\[Transpose] . A . 
      A\[Transpose]], 
    Norm[A . A . A . A . A\[Transpose] . A\[Transpose] . 
      A\[Transpose] . A\[Transpose]]}
   );
dvals = Range[100, 200, 10];
funcs = {Norm[#, "Frobenius"] &, Norm, Tr};
sf = "Log";
dec[pairSeq_] := {{dvals, pairSeq[[All, 1]]}\[Transpose], {dvals, 
     pairSeq[[All, 2]]}\[Transpose]};
f = Norm;
plotFunc[f_, fname_, sampler_] := (
   ListLinePlot[dec[getVal[#, f, sampler] & /@ dvals], 
    PlotLabel -> fname, AxesLabel -> {"d", "value"}, 
    PlotLegends -> {"f(AA'AA'AA'AA')", "f(AAAAA'A'A'A')"}, 
    ScalingFunctions -> "Log"]
   );
randNormal[d_] := RandomVariate[NormalDistribution[], {d, d}];
randUniform[d_] := RandomVariate[UniformDistribution[], {d, d}];
randBernoulli[d_] := 
  N@RandomVariate[BernoulliDistribution[0.5], {d, d}];
sampler = randNormal;
TableForm[{{plotFunc[Norm, "f(A)=||A||", sampler],
    plotFunc[Tr, "f(A)=Tr(A)", sampler],
    plotFunc[Norm[#, "Frobenius"] &, 
     "f(A)=||A!(*SubscriptBox[(||), (F)])", 
     sampler]}}[Transpose]]

Our of curiosity, what do these plots looks like if you divide through by $d^2$? Is the (de)correlation effect relatively constant or can you see it changing as the dimension increases? — whpowell96, Feb 19 '24 at 19:19
@whpowell96 The standard normalization is to divide entries by sqrt(d) because that ensures norm(A) is independent of dimension. This also carries over to norm(AAA...) so the plots are flat — Yaroslav Bulatov, Feb 19 '24 at 19:27
@Hyperplane for $d=2$ we have $\langle\text{Tr}\left[A.A.A^T.A^T\right]\rangle=12, \langle\text{Tr}\left[A.A^T.A.A^T\right]\rangle =20$ — Yaroslav Bulatov, Feb 19 '24 at 19:31
@BenGrossmann for unitarily invariant norms as a measure of "larger", the original question is equivalent to asking -- what's larger $|A|^2$ or $|A^2|$ — Yaroslav Bulatov, Feb 20 '24 at 07:12
@YaroslavBulatov Ah, well done. That seems obvious in retrospect — Ben Grossmann, Feb 20 '24 at 12:21
@YaroslavBulatov And in case you somehow haven’t put it together from there, unitarily invariant norms are necessarily submultiplicative so the reformulated question has a quick answer. — Ben Grossmann, Feb 20 '24 at 12:26
I had a feeling that this followed necessarily from submultiplicativity, but I wonder if that fact can derive the progression of norms in terms of the equidistrubtion of $A$ and $A^T$ in the product or the ratio of the maximal and minimal norms, which seems to be approaching 2 — whpowell96, Feb 20 '24 at 15:31
@JimB it came out from an original question for finding formulas for Gaussian expression (that is still ongoing), but in this case Gaussian or non-Gaussian doesn't matter, this follows from polar decomposition + properties of generic matrices — Yaroslav Bulatov, Mar 17 '24 at 15:21

score 6 · Answer 1 · answered Feb 19 '24 at 20:38

If the entries are $a_{ij}$, $$\text{Tr}\left(A^4 (A^T)^4\right) = \sum_{i_1 i_2 \ldots i_8} a_{i_1 i_2} a_{i_2 i_3} a_{i_3 i_4} a_{i_4 i_5} a_{i_6 a_5} a_{i_7 i_6} a_{i_8 i_7} a_{i_1 i_8}$$ while $$ \text{Tr}\left((A A^T)^4\right) = \sum_{i_1 i_2 \ldots i_8} a_{i_1 i_2} a_{i_3 i_2} a_{i_3 i_4} a_{i_5 a_4} a_{i_5 i_6} a_{i_7 i_6} a_{i_7 i_8} a_{i_1 i_8}$$ But if the entries are iid standard normal the only terms whose expected value is nonzero are those where the eight factors are equal in pairs. For example, for a nonzero term in $\text{Tr}\left(A^4 (A^T)^4\right)$ you could have $a_{i_1 i_2} = a_{i_3 i _4}$, $a_{i_2 i_3} = a_{i_1 i_8}$, $a_{i_3 i_4} = a_{i_8 i_7}$, and $a_{i_4 i_5} = a_{i_6 i_5}$. But that would require all $i_k$ to be equal. It seems the second form allows more possibilities than the first. It should be possible (if rather tedious) to enumerate them.

Yaroslav Bulatov · Answer 2 · 2024-02-23T20:47:44.397

Proof outline:

Restrict attention to $|M|$ where $MM^T=|M|^2$, aka the "matrix absolute value" or the "P.S.D term of the polar decomposition".

We want to know whether $|AAA^TA^T|$ is larger than $|AA^TAA^T|$.

$|AAA^TA^T|=|A^2|^2$
$|AA^TAA^T|=|A|^4$.

Now we want to know which one is larger, $|A|^2$ vs $|A^2|$. Using polar decomposition of $A=|A|\cdot U$ we have

$|A^2|=|A|\cdot U\cdot |A|$
$|A|^2=|A| \cdot |A|$.

The latter is larger because $U$ rotation matrix breaks correlations. Consider $2\times 2$ matrix whose polar decomposition is "double first coordinate, then rotate by 90 degrees", we have

$\operatorname{norm}(|A|\cdot|A|)=4$
$\operatorname{norm}(|A|\cdot U\cdot|A|)=2$

Why is $AA^TAA^TAA^TAA^T$ larger than $AAAAA^TA^TA^TA^T$ for Gaussian $A$?

2 Answers2