Good evening,
We were playing with a friend on Desmos, and we came to $x \longmapsto \arctan\left(\exp\left(-\displaystyle\frac{1}{\sqrt{1-x^2}}\right) \right)$. Here is the graph :
And we have :
$$\int_{-1}^1 \arctan\left(\exp\left(-\displaystyle\frac{1}{\sqrt{1-x^2}}\right) \right) \hspace{0.1cm} \mathrm{d}x \approx 0.529797566526076$$
We were wondering if it was calculable ? There is very few chance but hey, we never know. Best regards.
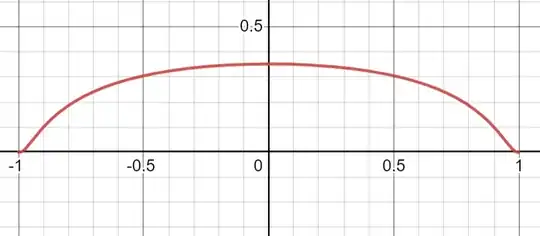
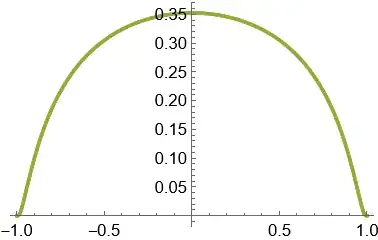
Expand using $\tan^{-1}$’s Maclaurin series and substitute $\frac1{\sqrt{1-x^2}}\to x$: $$\int_{-1}^1 \tan^{-1}\left(\exp\left(-\frac{1}{\sqrt{1-x^2}}\right) \right) dx=2\sum_{n=0}^\infty\frac{(-1)^n}{2n+1}\int_1^\infty \frac{e^{-(2n+1)}}{x^2\sqrt{x^2-1}}dx$$
One apply @Metamorphy’s method in this answer, by using $\int_0^\infty e^{ax}da=\frac{e^x}x$ twice, and “generalized” Meijer G:
$$\int_1^\infty \frac{e^{-(2n+1)x}}{x^2\sqrt{x^2-1}}dx=\int_{2n+1}^\infty\int_b^\infty\int_1^\infty\frac{e^{-ax}}{\sqrt{x^2-1}}dx\,da\,db= \int_{2n+1}^\infty\int_b^\infty K_0(a)\,da\,db= \frac12\int_{2n+1}^\infty\int_b^\infty G_{0,2}^{2,0}\left(\frac a2,\frac12;0,0\right)\,da\,db$$
Now apply its integration formula to get
$$\int_1^\infty \frac{e^{-(2n+1)x}}{x^2\sqrt{x^2-1}}dx =2-(2n+1)\pi+G_{2,4}^{2,2}\left(\left(n+\frac12\right)^2;^{\ \ \ 1,\frac32}_{1,1,0,\frac12}\right)$$
after converting to the ordinary Meijer G function. Numerically, plugging in $\infty$ after integrating with respect to $b$ gives $2$. Therefore:
$$\boxed{\int_{-1}^1 \tan^{-1}\left(\exp\left(-\frac{1}{\sqrt{1-x^2}}\right) \right) dx=\frac{(2-\pi)\pi}4+\sum_{n=0}^\infty\frac{(-1)^n}{2n+1}\left(G_{2,4}^{2,2}\left(\left(n+\frac12\right)^2;^{\ \ \ 1,\frac32}_{1,1,0,\frac12}\right)-2\pi n\right)}$$
shown here:
Unfortunately the Leibniz formula $\frac\pi4=\sum\limits_{n=0}^\infty\frac{(-1)^n}{2n+1}$ converges slowly, so everything must be in the sum to numerically test it. Also, if Wolfram Cloud calculates about $20+$ terms, numerical errors appear, so more working precision is needed. However, the sum quickly converges.
The arctan of the exponential is a famous function, antiderivative of sech, eg as soliton solutions of the sine-Gordon equation
Plot[{ArcTan[E^(-1/Sqrt[1 - x^2])],
\[Pi]/4 - ArcTan[Tanh[1/(2 Sqrt[1 - x^2])]],
\[Pi]/4 - 1/2 Gudermannian[1/Sqrt[1 - x^2]]} , {x, -1, 1}]
But no luck integrating algebraically.
We can find a numerical approximation (maybe there's an analytical solution) for the integral using consecutive series expansions though it is not too helpful. In view that $x\in(-1,1)$, the series expansion centered at $x=0$ of $(1-x^2)^{-1/2}$ would converge since it has a radius of convergence of $1$. Then, the series expansion of the exponent converges for all $(1-x^2)^{-1/2}$ and its image would be $[0,1/e]$ for $x\in(-1,1)$ in turn meaning that the series expansion of $\arctan(\exp(…))$ will converge too because its radius of convergence is $\pi/2$ centered at $0$.
$$\begin{aligned} &\int_{-1}^1\arctan\left(\exp\left(-\frac{1}{\sqrt{1-x^2}}\right)\right)\text dx=\\ &=\int_{-1}^1\sum_{k=0}^\infty\frac{(-1)^k}{2k+1}\exp\left(-\frac{2k+1}{\sqrt{1-x^2}}\right)\text dx\\ &= \int_{-1}^1\sum_{k=0}^\infty\frac{(-1)^k}{2k+1} \sum_{n=0}^\infty\frac{(-1)^n(2k+1)^n}{n!}(1-x^2)^{-\frac{n}{2}}\text dx\\ &= \int_{-1}^1\sum_{k=0}^\infty \sum_{n=0}^\infty\frac{(-1)^{n+k}(2k+1)^{n-1}}{n!}\sum_{m=0}^\infty{-n/2 \choose m}(-1)^mx^{2m}\text dx\\ &= \sum_{k=0}^\infty \sum_{n=0}^\infty \sum_{m=0}^\infty\frac{(-1)^{n+k+m}(2k+1)^{n-1}}{n!}{-n/2 \choose m}\int_{-1}^1x^{2m}\text dx\\ &= 2\sum_{k=0}^\infty \sum_{n=0}^\infty \sum_{m=0}^\infty\frac{(-1)^{n+k+m}(2k+1)^{n-1}}{n!(2m+1)}{-n/2 \choose m}\\ &= 2\sum_{k=0}^\infty \sum_{n=0}^\infty \sum_{m=0}^\infty\frac{(-1)^{n+k+m}(2k+1)^{n-1}}{n!m!(2m+1)}\frac{\Gamma(1-\frac{n}{2})}{\Gamma(1-\frac{n}{2}-m)}. \end{aligned} $$
