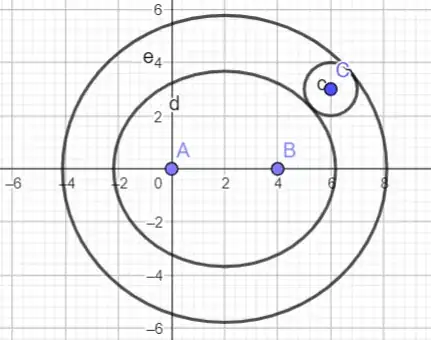
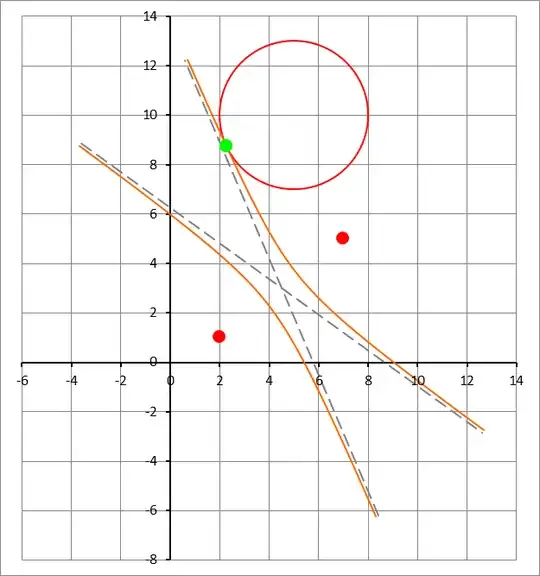
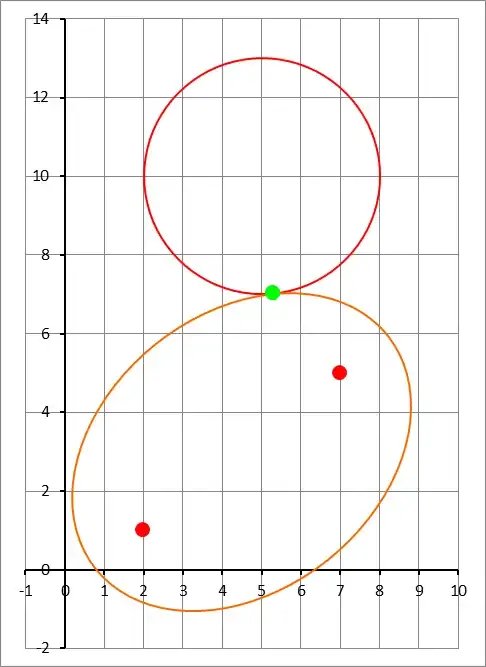
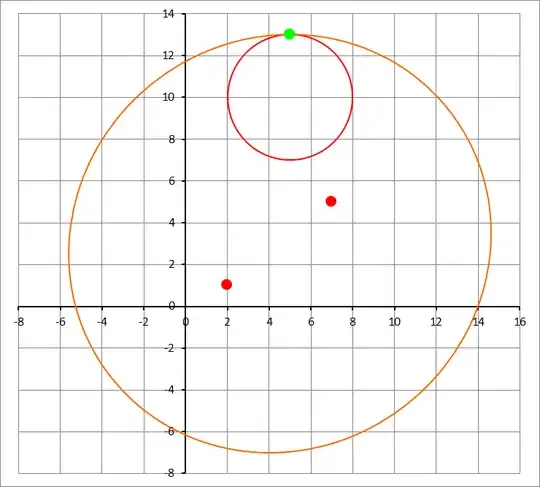
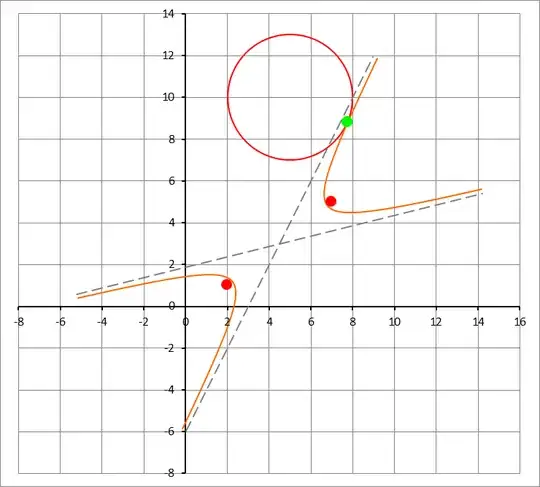
Given two points $F_1$ and $F_2$ and a circle centered at $r_0$ with radius $s$, I'd like to construct the ellipse with foci $F_1$ and $F_2$ that is tangent to the given circle. That is the question.
My attempt:
Let $r = [x, y]^T $ be the position vector of a point in the plane. To simplify the analysis, I'll introduce a new coordinate reference with its origin at the center of the ellipse. This is known, because the center of the ellipse is just the midpoint of the two foci. So let
$ C = \dfrac{1}{2} (F_1 + F_2) $
And define the unit vector
$ u_1 = \dfrac{ F_2 - F_1}{\| F_2 - F_1 \| } $
And let $u_2 $ be a unit vector that is perpendicular to $u_1$. Now define the rotation matrix
$ R = [u_1, u_2] $
By letting the $x'$ axis point along $u_1$ and the $y'$ axis point along $u_2$ , then if $p' = (x',y')$ is the local coordinate of a (world) point $p$ with resepct to this new frame, then then two vectors are related by
$ p = C + R p' $
So that
$ p' = R^T (p - C) $
Using these new coordinates, the two foci are now at $F'_1 = (-c, 0)$ and $F'_2 = (c, 0) $. Similarly, the given center of the circle can be computed as $r'_0 = R^T (r_0 - C) $
Now the equation of the ellipse to be found is
$ \dfrac{x^2}{a^2} + \dfrac{y^2}{a^2 - c^2} = 1 $
where $a^2 $ is unknown.
Let $(x_1, y_1)$ be the tangent point with the circle, then $(x_1, y_1)$ satisfies
$ \dfrac{x_1^2}{a^2} + \dfrac{y_1^2}{a^2 - c^2} = 1 \tag{1}$
$ (x_1 - {r'}_{0x} )^2 + (y_1 - {r'}_{0y} )^2 = s^2 \tag{2}$
And in addition to these two, we have that the gradients are along the same direction, which means
$ ( \dfrac{x_1}{a^2} , \dfrac{y_1}{a^2 - c^2} ) = K ( x_1 - r'_{0x} , y_1 - r'_{0y} ) $
So that
$ \dfrac{1}{a^2} \bigg( x_1 ( y_1 - r'_{0y} ) \bigg) - \dfrac{1}{a^2 - c^2} \bigg( y_1 (x_1 - r'_{0x} ) \bigg)= 0 \tag{3}$
Simplifying $(3)$, it becomes,
$ (a^2 - c^2) \bigg( x_1 y_1 - x_1 r'_{0y} \bigg) - a^2 \bigg( x_1 y_1 - y_1 r'_{0x} \bigg) = 0 $
And further into
$ - c^2 x_1 y_1 + (c^2 - a^2) x_1 r'_{0y} + a^2 y_1 r'_{0x} = 0 \tag{4}$
Equation $(1)$ also simplifies to
$ (a^2 - c^2) x_1^2 + a^2 y_1^2 = a^2 (a^2 - c^2) \tag{5}$
And equation $(2)$ when expanded and re-arranged, becomes
$ x_1^2 + y_1^2 - 2 x_1 r'_{0x} - 2 y_1 r'_{0y} + {r'_{0x}}^2 + {r'_{0y}}^2 - s^2 = 0 \tag{6} $
From this equation, it follows that
$ x_1^2 + y_1^2 = 2 x_1 r'_{0x} + 2 y_1 r'_{0y} + s^2 - {r'_{0x}}^2 - {r'_{0y}}^2 $
Substituting this into $(5)$, it becomes,
$ a^2 ( 2 x_1 r'_{0x} + 2 y_1 r'_{0y} + s^2 - {r'_{0x}}^2 - {r'_{0y}}^2 ) - c^2 x_1^2 =a^2 (a^2 - c^2) \tag{5'} $
Finally, let's define $A = a^2$ , then our three equations become
$ x_1^2 + y_1^2 = 2 x_1 r'_{0x} + 2 y_1 r'_{0y} + s^2 - {r'_{0x}}^2 - {r'_{0y}}^2 \tag{7}$
$ A ( 2 x_1 r'_{0x} + 2 y_1 r'_{0y} + s^2 - {r'_{0x}}^2 - {r'_{0y}}^2 ) - c^2 x_1^2 =A (A - c^2) \tag{8} $
$ - c^2 x_1 y_1 + (c^2 - A) x_1 r'_{0y} + A y_1 r'_{0x} = 0 \tag{9}$
Equations $(7),(8), (9)$ are quadratic in the variables $x_1, y_1$ and $A$.
Using Mathematica or Sage Math these three nonlinear equations (equations $(7),(8),(9)$) can be solved and the value(s) of $a$ obtained.
Important Remark: Now that we have a procedure for finding the tangent ellipse to a given circle (given the two foci of the ellipse to be found), then we have also solved the problem of finding the tangent ellipse to a given ellipse (given the two foci of the ellipse to be found). This follows from the fact that we can linearly transform the given ellipse (by an affine transformation) and turn it into a circle, and together with it of course we transform the two given points, then the problem reduces to the current setup.