1

(Graph homology, from this Wikipedia page: https://en.wikipedia.org/wiki/Graph_homology)

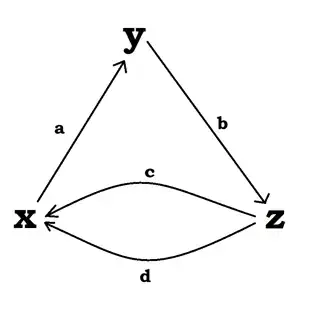
I'm interested in the full Cayley table and geometric representation of the free abelian group $\mathfrak C_1$ generated on a graph $$\mathfrak G = \bigg( x \xrightarrow{\quad a \quad} y \xrightarrow{\quad b \quad} z \xrightarrow{\quad c, d \quad} x \bigg)$$

Which can be drawn as

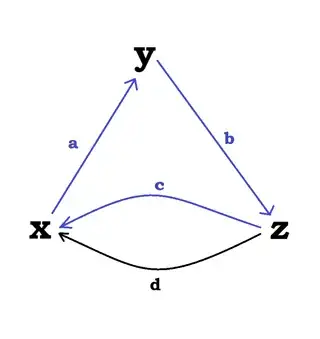
enter image description here

Wikipedia adds a group structure to the edges such that we have $\mathfrak C_1 = \big( \{ a, b, c, d \}, + \big)$. Let blue (positive) be the clockwise direction for the edges, and red (negative) be the direction corresponding to counter-clockwise. Of course, we don't need this orientation for the graph, but it corresponds to what's in the figure. An obvious expression would be $a + b + c $, which is just going in a loop around the graph:

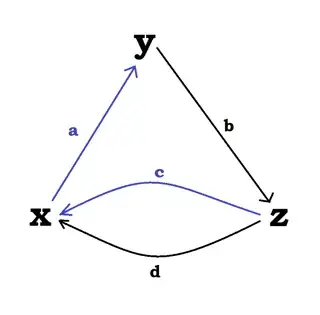
enter image description here

More challenging geometrically would be $a + c$, as these two elements are not "connected" as end-to end:

enter image description here

You could try to "abuse" commutativity, and have $a + c = c + a = $ "The path from z to y", but it already feels like shaky ground.

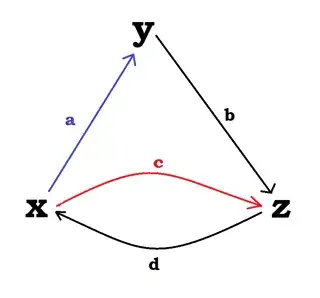
Now, have $a - c$

enter image description here

These paths "diverge" and point to two different places, yet by the group axioms there must be some element within the group that they point two. I'd like two things if possible, which can either be provided by a user or can have a link to their information shared:

(i)

What group is this? Is there a full Cayley table available online that I can look at?

(ii)

What is the geometric interpretation of each element in the Cayley table? What underlying geometric property gives rise to the fact that this is an abelian group? I'd prefer no answers to this question rather than answers that try to claim it's only a formal operation, as those answers tend to be wrong.

Thanks in advance for any helpful links.

Nate
  • 1,651
  • Do you know what a free abelian group is? – Randall Feb 10 '24 at 02:20
  • Curious: why are answers that claim it's only a formal operation "wrong"? That is quite literally the way one defines a free object from a generating set from scratch, and is pretty foundational to gobs of modern mathematics, even though it's "only" a formal operation. – Randall Feb 10 '24 at 02:24
  • @Randall Most formal operations break or lead to contradictions when done blindly. Formal operations that tend to "work" have a geometric foundation that they are based off of (but people forget about). Off the top of my head see how the dot product or the actions of differential forms distribute linearly. A geometric foundation that preceded the formal description/abstraction (bad) geometers learned the formal operation, but forgot the geometric part. "Modern" refers to Bourbaki/Hilbert-style mathematics, which is part of a failed paradigm that great mathematicians (Arnold) were opposed to. – Nate Feb 10 '24 at 02:36
  • The geometry won't enter the picture until you take homology. But to get there, you need the formalism of free abelian groups. – Randall Feb 10 '24 at 02:40
  • @Randall Misunderstanding I think. I see what you were concerned about. I already know what a free abelian group is. Lattice-like structure where any element $\mathbf w = z_1 ; \mathbf u + z_2 , \mathbf v$ such that $z_1 , z_2 \in \mathbb Z$. Off of that I want to understand the visualization/geometry of the structures generated by the group. Since visualization methods are sometimes "lost" (as observed by Arnold , Von Neuman, etc...) I'd prefer no answer if a person doesn't know it, rather then them trying to claim it's just a formal operation. – Nate Feb 10 '24 at 02:42
  • Your free abelian group $\mathfrak{C}_2$ is not the 4-point set ${a,b,c,d}$. Instead, it's the free abelian group on that set. – Randall Feb 10 '24 at 02:45
  • @Randall That's defined in my problem statement, no? "Wikipedia adds a group structure to the edges such that we have $\mathfrak C_2 = \big( { a, b, c, d} , + \big)$." Concerns with how I defined it? – Nate Feb 10 '24 at 02:47
  • 1
    I'll let someone else--better at explaining--jump in. – Randall Feb 10 '24 at 02:48
  • WP says "Define $C_2$ as the free abelian group generated by the set of two-dimensional cells". Before that they add $A$ on the edges $c,d$ and consider an abstract simplicial complex (not a graph). Note that the arrow directions make the cell an oriented cycle, i.e. $c-d$, not $c+d$. Did you mean $C_1$ instead? It is a free Abelian group on 4 elements (just isomorphic to $\Bbb Z^4$), that's a countable group so I doubt anyone could post a Cayley table of it :-) – Amateur_Algebraist Feb 10 '24 at 08:01
  • 1
    @Amateur_Algebraist Thanks for noticing the typo. Corrected. – Nate Feb 10 '24 at 09:07
  • @Amateur_Algebraist I don't know what the lingua for representing group structures in latex, so bear with me (and I hope you can understand this). Let $\ggg$ denote an order from left to right. The elements of $\mathbb Z^4$ in increasing order are given as $\big( 0 \ggg 1 \ggg 2 \ggg 3 \big)$. Let $I$ be the isomorphism between groups. Would it hold that $I(0) = (0), I(1) = a, I(2) = b, I(3) = c$? Then what would map to $d$? – Nate Feb 10 '24 at 09:11
  • No, sorry, for now I don't get what you mean. There's no innate ordering on an abstract group or its generators. $\Bbb Z^4$ is the lattice of integer points of $\Bbb R^4$, it has infinitely many 4-element "bases" (minimal generating sets); mapping $a,b,c,d$ to any of them gives a group isomorphism $\Bbb Z^4 \leftrightarrow C_1$. We can take a specific one and work with it, e.g. $a \mapsto (1,0,0,0), \ldots, d \mapsto (0,0,0,1)$. But even from the 'geometrical' standpoint there is no reason to prefer $a$ to $b$ in the graph to place it higher on the list, so there is no 'canonical' isomorphism. – Amateur_Algebraist Feb 10 '24 at 10:56
  • 2
    There is a lot of geometric motivation for (simplicial, singular) homology. I admit it's a bit lost from modern sources. I don't go into all of it but maybe this helps – FShrike Feb 10 '24 at 11:27
  • I'll look at it, thanks! – Nate Feb 10 '24 at 13:23

0 Answers0