0

For a large real-valued random matrix, eigenvalues follow the circular law, but for small matrices, there's a preference towards the real line. How can I upper bound this probability?

enter image description here For instance suppose $M$ is a $d\times d$ matrix with IID Gaussian entries with mean 0 and variance $1/d$, here are sample probabilities :

$$ \left( \begin{array}{ccc} & \text{d} & \text{p(real)} \\ & 2 & 0.7146 \\ & 3 & 0.3553 \\ & 4 & 0.1184 \\ & 5 & 0.0351 \\ & 6 & 0.0052 \\ & 7 & 0.001 \\ \end{array} \right) $$

fractionReal[d_] := (numSamples = 10000;
   mat := RandomVariate[NormalDistribution[0, 1/Sqrt[d]], {d, d}];
   mats = Table[mat, {numSamples}];
   evals = Eigenvalues /@ mats;
   allReal[list_] := AllTrue[list, RealValuedNumberQ];
   N@Mean[Boole[allReal /@ evals]]);
TableForm@Table[{d, fractionReal[d]}, {d, 2, 7, 1}]

d = 2;
numSamples = 10000;
mat := RandomVariate[NormalDistribution[0, 1/Sqrt[d]], {d, d}];
mats = Table[mat, {numSamples}];
evals = Eigenvalues /@ mats;
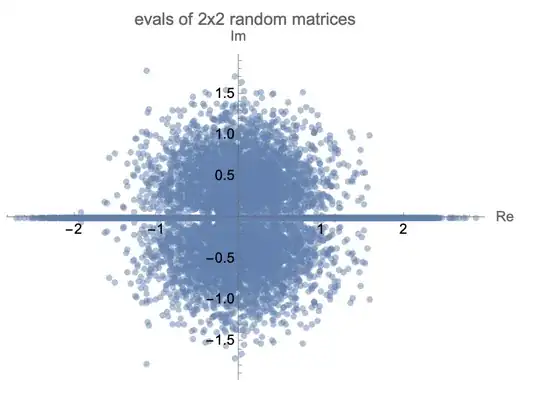
ComplexListPlot[Flatten@evals, 
 PlotLabel -> "evals of 2x2 random matrices", 
 AxesLabel -> {"Re", "Im"}, 
 PlotStyle -> Directive[Opacity[.5], PointSize[Medium]]]
Yaroslav Bulatov
  • 5,579
  • I think this is related. https://mathoverflow.net/questions/372115/random-matrices-having-all-real-eigenvalues-uniform-vs-gaussian-distributions – Vezen BU Feb 15 '24 at 07:40
  • See also https://math.stackexchange.com/questions/3770846/probability-for-an-n-times-n-matrix-to-have-only-real-eigenvalues – Vezen BU Feb 15 '24 at 07:41

0 Answers0