Context
I found an extra-hard (but fake) example of a paper which adheres to the syllabus for the hardest mathematics high school course available in the state of NSW in Australia; Mathematics Extension 2. Question 16 (a) has caught my eye and I'm having difficulty solving it, so am looking for tips. I will reproduce the question entirely below and add explain where I am up to.
Question Statement
$16 (a)$ $[\mathbf7$ $\mathbf{marks}]$ A sequence $x_1, x_2, x_3, \dots$ of positive real numbers is given, recursively defined by $x_1=1$ and $x_{n+1} = \frac{1}{x_1^2 + x_2^2 + \dots + x_{n}^2}$ for each $n > 1$.
$(i)$ $[\mathbf2]$ Show that $x_n \leq \frac{1}{\sqrt[3]{n-1}}$ for each $n\geq2$.
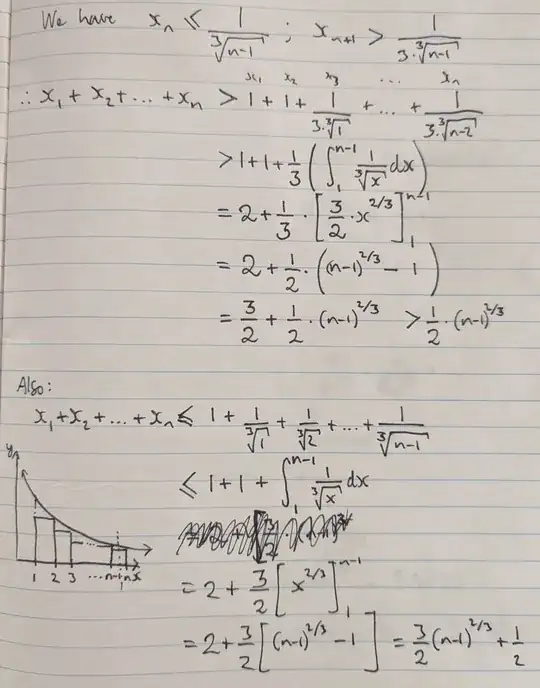
$(ii)$ $[\mathbf1]$ Prove that every integer $n\geq2$ satisfies $\frac{1}{2^{2/3}} + \frac{1}{3^{2/3}} + \dots + \frac{1}{n^{2/3}} \leq \int_1^nx^{-2/3}dx$, and hence show that $x_{n+1} > \frac{1}{3\sqrt[3]{n-1}}$ for each integer $n\geq2$.
$(iii)$ $[\mathbf1]$ Prove that every $n\geq2$ also satisfies $\frac{1}{\sqrt[3]{1}} + \frac{1}{\sqrt[3]{2}} + \dots + \frac{1}{\sqrt[3]{n}} \geq \int_1^{n+1}\frac{1}{\sqrt[3]{x}}dx$, and hence deduce that $x_1 + x_2 + \dots + x_n > \frac{(n-1)^{2/3}}{2}$ for each $n\geq2$.
$(iv)$ $[\mathbf1]$ By considering a similar integral in $(iii)$, show that for all sufficiently large positive integers $n$ the inequality $\frac{1 - \frac{1}{2019}}{2} < \frac{x_1 + x_2 + \dots + x_n}{n^{2/3}} < \frac{3 + \frac{1}{2019}}{2}$ holds.
$(v)$ $[\mathbf2]$ It is given ($\mathbf{Do}$ $\mathbf{NOT}$ $\mathbf{prove}$) that the limit $\lim\limits_{n \to \infty} \frac{x_1 + x_2 + \dots + x_n}{n^{2/3}}$ exists, and is equal to a positive real number $C$.
Show that $C = \frac{\sqrt[3]{9}}{2}$.
Attempt so far
I was able to solve parts (i), (ii) and (iii) and am able to solve the lower bound in (iv) but cannot find a good integral for the upper bound. (My problem is trying to make n+1 appear in the integrand, while also only using n Riemann sums for the bound). I also see issues with applying squeeze law in (v).
Request For Hint
What is a good hint for finding the correct integral in (iv), and how do I extend this to part (v) where I'm hoping squeeze law applies but can't see a trivial path forward if the two integral bounds have multipliers of $\frac{1}{2}$ and $\frac{3}{2}$ respectively (thereby squeezing to a range rather than a point).
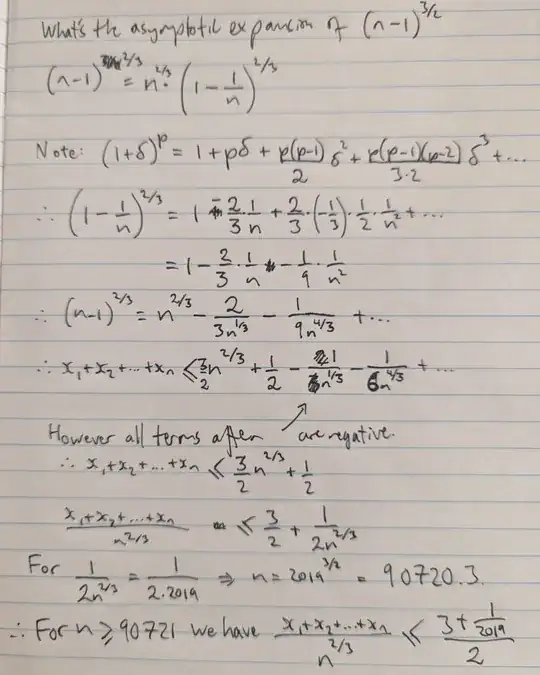
I'm wondering if there's a more elementary method though, as parts (i)-(iv) were not needed to use the theorem; and perhaps there's a nicer thing there.
– Juan Reight Deag Feb 03 '24 at 10:39Were there better Riemann sums (or otherwise) for (iv). I had to go back to asymptotic analysis to demonstrate that the extra constant bit was sufficient (which is a little too advanced). For the lower bound you can just directly solve for n using $\frac{(n-1)^{2/3}}{2n^{2/3}} = \frac{1 - \frac{1}{2019}}{2}$, which is a high school technique.
Maybe that's the (troll) point!
– Juan Reight Deag Feb 03 '24 at 21:48