2

At first sight, the following series expression seems to converge everywhere:

$$f(s) = \sum_{n=2}^\infty \frac{\zeta(n)-1}{n^s + n^{1-s}} \tag{1}$$

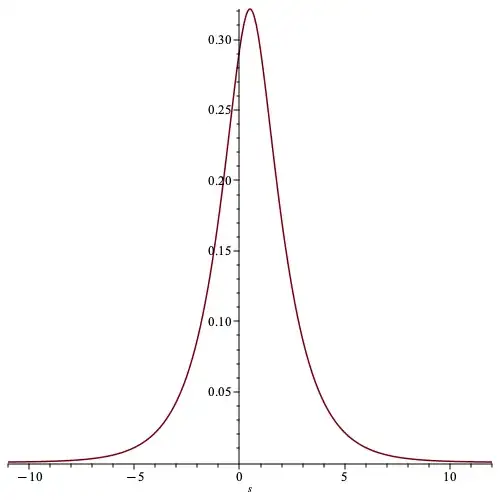
For $s$ real we obtain a nice Gaussian shaped curve:

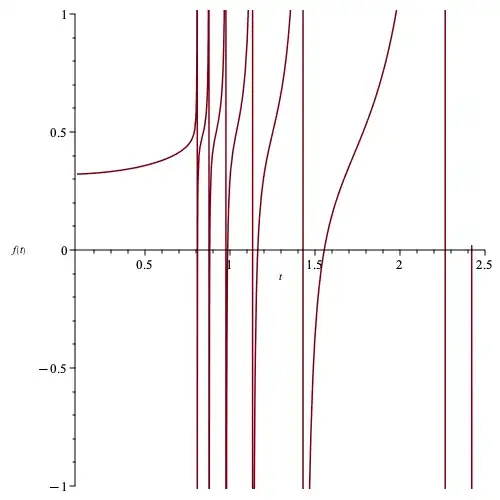
enter image description here

however for $s=\frac12 + ti, N = 6$ we get (note the graph quickly becomes 'messier' for higher $N$):

enter image description here

The location of the infinite number of poles can be easily explained. These are induced when $n^s + n^{1-s}=0$ for a certain integer $n$ and this can only occur when $\Re(s)=\frac12$.

From the graph we can also see some roots lying between the poles and based on (limited) numerical evidence I like to conjecture that these also all reside on the critical line $\Re(s)=\frac12$. Could the latter be within reach of a proof (my hope is that this is somehow related to the location of the poles) or will this be just as hard as the RH?

Agno
  • 3,231
  • 15
  • 19
  • To me it looks like poles are dense on the line $1/2$ so the function is not defined there; there is a function to the right and a symmetric one to the left of the line but they both seem to have that line as natural boundary – Conrad Jan 28 '24 at 19:55
  • underrated. And btw looks alot like one of my own zeta function questions posted ! – mick Sep 10 '24 at 22:54
  • https://math.stackexchange.com/questions/4622671/roots-and-analytic-continuation-of-ts-sum-n0-ns-n-s-1

    Similar looking like I said

     – mick Sep 10 '24 at 23:08

0 Answers0