6

Recently, I was working on some olympiad geometry problems, and I noticed that if two points $A,B$ are fixed on a circle $\omega$, then a variable point $C$ on $\omega$ defines a set of orthocentres of $\Delta ABC$, and they appear to be on a circle (which also passes through $A,B$).

An image from a reproduction on GeoGebra is below (orthocentres are $I,D,J,H$):

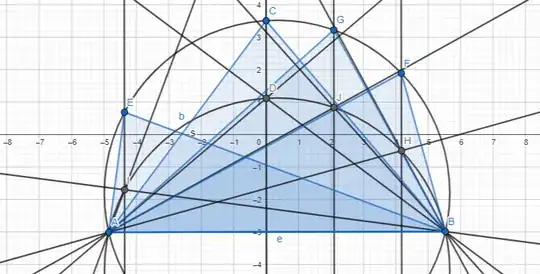
enter image description here

I have tried to prove this using similarity, congruence, circle theorems, Euler line, etc., but haven't been able to make progress.

Does anyone know of a proof of this or the name of the theorem, if it exists?

TheMathsPerson
  • 93
  • 1
    For a "one-idea" proof, (it is well-known) show that $CH = 2 OD$ (even as vectors), where $O$ is the circumcenter and $D$ is the midpoint of $AB$. Hence, the loci of orthocenter is the circle $\omega$ shifted down by $2OD$, and in particular have the same radius. (This is hinted at in OP's diagram.) – Calvin Lin Jan 27 '24 at 05:10
  • 1
    For another proof, recall that the reflection of $H$ across $AB$ lies on the circumcircle. Hence, the locus of $H$ is the reflection of the circumcircle across $AB$, thus is a circular arc (again of the same radius). – Calvin Lin Jan 27 '24 at 05:16

1 Answers1

8

Let $C$ be an arbitrary point on $\omega$; let $AD$, $BE$, $CF$ be the altitudes of $\triangle ABC$ and let $H$ be their intersection.

We have $\angle AHF = \angle DHC = 90^\circ - \angle DCH = 90^\circ - \angle BCH$, the first by vertical angles and the second by complementary angles in a right triangle. Similarly, $\angle FHB = \angle CHE = 90^\circ - \angle HCE = 90^\circ - \angle HCA$. Putting these together, we get $$\angle AHB = \angle AHF + \angle FHB = 180^\circ - (\angle BCH + \angle HCA) = 180^\circ - \angle BCA.$$

Since $C$ lies on $\omega$, we know that $\angle BCA$ is constant (and is half the measure of the arc $AB$ that does not contain $C$). Therefore $\angle AHB$ is also constant, no matter how $C$ moves - which is exactly what we need to know that $H$ lies on a circular arc through $AB$.

(More precisely, that's what happens if $C$ stays on the same arc in $\omega$: in the picture, if $C$ stays above chord $AB$. If $C$ goes to the other arc, then $\angle BCA$ is replaced by its supplement $180^\circ - \angle BCA$,and so $\angle AHB$ is also replaced by its supplement. In that case, the orthocenter $H$ exactly traces out the other arc of the circle it was on before.)

Misha Lavrov
  • 159,700
  • 2
    It is worth pointing out that what you have shown is that the locus is the reflection of $\omega$ along line $AB$. $\quad$ And that follows an immediate corollary of the well-known fact that the reflection of $H$ along $AB$ lies on the circumcircle, which is often shown by the same angle chasing proof that you've done. (OP is asking if this is a theorem). – Calvin Lin Jan 27 '24 at 05:15