On two concentric balls and a closed set; Bridges

Question

In Bridges' Foundations of Real and Abstract Analysis, I read about the following theorem.

(5.2.2) Proposition. Let $S$ be a nonempty closed subset of the Euclidean space $\mathbb R^N$ such that each point of $\mathbb R^N$ has a unique closest point in $S$. Then $S$ is convex.

This theorem is proved by contradiction and to invoke the contradiction, the author relies on a previous exercise which I simply can not fathom. If anyone knows what the gist of this is about, and knows how to prove it, I'd be very grateful for some guidance. The exercise reads as follows:

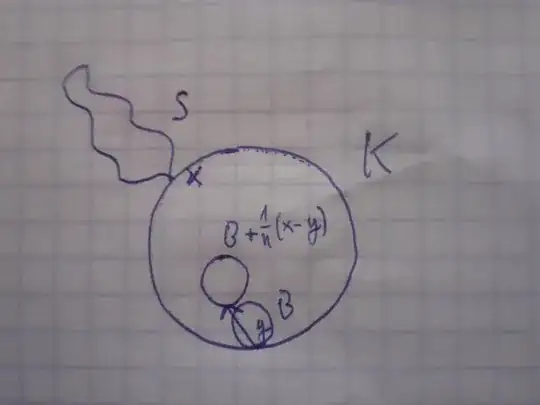
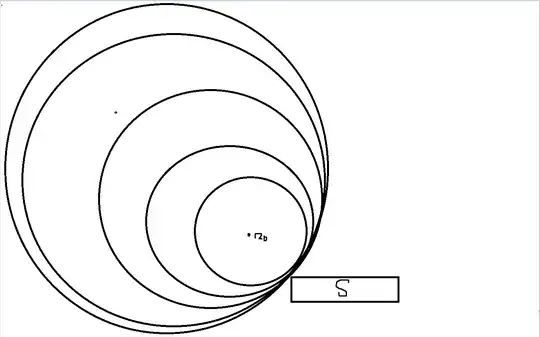
(4.3.7.7) Let $S$ be a nonempty closed subset of $\mathbb R^N$, and $K,B$ closed balls in $\mathbb R^N$ such that (i) $B\subset K$ and (ii) $K$ intersects $S$ in a single point $x$ on the boundary of $K$. If $B$ does not intersect the boundary of $K$, let $y$ be the centre of $B$; otherwise, $B$ must intersect the boundary of $K$ in a single point, which we denote by $y$. For each positive integer $n$ let $$K_n=\frac1{n}(y-x)+K.$$ Prove that for sufficiently large $n$ we have $B\subset K_n$ and $K_n\cap S=\emptyset$. Hence prove that there exists a ball $K'$ that is concentric with $K$, has radius greater than that of $K$, and is disjoint from $S$.

(For the first part, begin by showing that there exists a positive integer $\nu$ such that $B\subset K_n$ for all $n\geq \nu$. Then suppose that for each $n\geq \nu$ there exists $s_n\in K_n\cap S$. Show that there exists a subsequence $(s_{n_k})$ converging to $x$, and hence find $k$ such that $s_{n_k}\in K\cap S$, a contradiction.)

Unfortunately, I haven't been able to find anywhere in the book if $\subset$ is proper inclusion or not. When the author writes $K_n=\frac1{n}(y-x)+K$, I take it to mean the set $K_n=\{\frac1{n}(y-x)+k:k\in K\}$.

I'm somewhat of a beginner to this and the exercise seems very unintuitive to me. If $K$ intersects $S$ at a single point, how can there be a ball, concentric with $K$, and radius greater than $K$, but that is disjoint from $S$?

---

As for trying to solve this exercise, let's suppose $B$ does not intersect the boundary of $K$, then define $d(z,B)=\inf \{ d(z,b):b\in B \}$. Let $z\in B-\frac{1}{n}(y-x)$, then by the triangle inequality $$d(z, K^c) \geq d\left(z+\frac{1}{n}(y-x), K^c\right) - d\left(z, z+\frac{1}{n}(y-x)\right)$$ The first term on the right is positive, because $z+\frac{1}{n}(y-x)$ is a point in $B$, i.e. in the interior of $K$, and a point belongs to the interior of a set if and only if the distance from the point to the complement is strictly positive. The second term is simply $\frac{1}{n}\lVert y-x\rVert$ and this can be made arbitrarily small. So $d(z, K^c)$ is positive and it follows that $z\in K^\circ \subset K$, so $B-\frac{1}{n}(y-x)\subset K$, i.e. $B\subset K+\frac{1}{n}(y-x)=K_n$.

I'm not sure if this proves the first part, but it remains to prove the case when $B$ does intersect $K$ and moreover, that $K_n\cap S=\emptyset$. The below picture is a sketch of the case when $B$ intersects $K$. The arrow denotes the vector $\frac{1}{n}(x-y)$.

---

EDIT: Here's the proof of the proposition above, word by word:

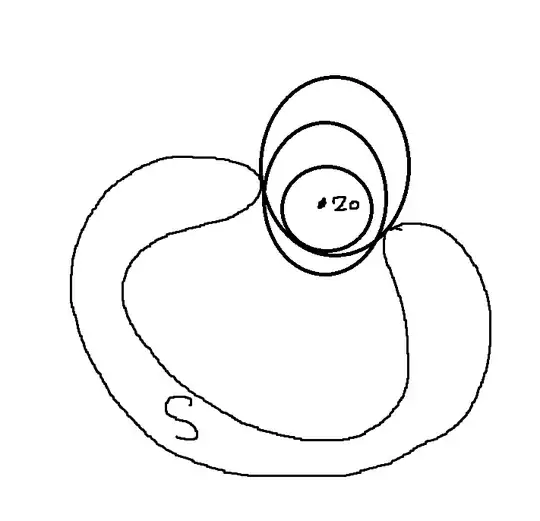
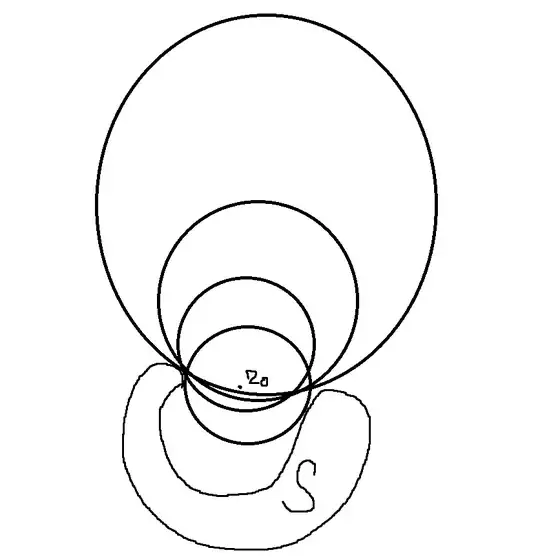
Proof. Supposing that $S$ is not convex, we can find $a,b\in S$ and $\lambda\in (0,1)$ such that $$z=\lambda a+(1-\lambda)b\not\in S.$$ Since $X\setminus S$ is open, there exists $r>0$ such that $\overline{B}(z,r)\cap S=\emptyset$. Let $\mathcal{F}$ be the set of all closed balls $B$ such that $\overline{B}(z,r)\subset B$ and $S\cap B^\circ=\emptyset$; then $\overline{B}(z,r)\in \mathcal{F}$. The radii of the balls belonging to $\mathcal{F}$ are bounded above, since any ball containing $B$ and having sufficiently large radius will meet $S$. Let $r_{\infty}$ be the supremum of the radii of the members of $\mathcal{F}$, and let $(\overline{B}(x_n,r_n))_{n=1}^\infty$ be a sequence of elements of $\mathcal{F}$ such that $r_n\to r_\infty$. Then $x_n\in \overline{B}(z,r_\infty)$ for each $n$. Since $\overline{B}(z,r_\infty)$ is compact (Theorem (4.3.6)) and therefore sequentially compact (Theorem (3.3.9)), we may assume without loss of generality that $(x_n)$ converges to a limit $x_\infty$. Let $K=\overline{B}(x_\infty,r_\infty)$; we prove that $K\in \mathcal{F}$.

First we consider any $x\in \overline{B}(z,r)$ and any $\epsilon>0$. Choosing $m$ such that $\lVert x_m-x_\infty\rVert<\epsilon$, and noting that $\overline{B}(z,r)\subset\overline{B}(x_m,r_m)$, we have \begin{align} \lVert x-x_\infty \rVert&\leq \lVert x-x_m\rVert +\lVert x_m-x_\infty\rVert \\ &<r_m+\epsilon\\ &\leq r_\infty+\epsilon. \end{align} Since $\epsilon$ is arbitrary, we conclude that $\lVert x-x_\infty\rVert\leq r_\infty$; whence $\overline{B}(z,r)\subset K$. On the other hand, supposing that there exists $s\in S\cap B(x_\infty,r_\infty)$, choose $\delta>0$ such that $\lVert s-x_\infty\rVert<r_\infty-\delta$, and then $n$ such that that $0\leq r_\infty-r_n<\delta/2$ and $\lVert x_n-x_\infty\rVert<\delta/2$. We have \begin{align} \lVert s-x_n \rVert&\leq \lVert s-x_\infty\rVert +\lVert x_\infty-x_n\rVert \\ &<r_\infty-\delta+\frac{\delta}{2} \\ &=r_\infty-\frac{\delta}{2} \\ &< r_n, \end{align} so $s\in S\cap B(x_n,r_n)$. This is absurd, as $B(x_n,r_n)\in\mathcal{F}$; hence $S\cap B(x_\infty,r_\infty)$ is empty, and therefore $K\in\mathcal{F}$.

Now, the centre $x_\infty$ of $K$ has a unique closest point $p$ in $S$. This point cannot belong to $K^\circ$, as $K\in\mathcal{F}$; nor can it lie outside $K$, as $r_\infty$ is the supremum of the radii of the balls in $\mathcal{F}$. Therefore $p$ must lie on the boundary of $K$. The unique closest point property of $S$ ensures that the boundary of $K$ intersects $S$ in the single point $p$. It now follows from Exercise (4.3.7:7) that there exists a ball $K'$ that is concentric with $K$, has radius greater than $r_\infty$, and is disjoint from $S$. This ball must contain $\overline{B}(z,r)$ and so belongs to $\mathcal{F}$. Since this contradicts our choice of $r_\infty$, we conclude that $S$ is, in fact, convex.

Answer 1

Ok, I finally understand this proof. I discuss this below, but you wanted to know about the exercise more than anything else. I am adamant that the "concentric with $K$" thing is wrong, but it is also unnecessary so let's put that to one side.

Let $B=B(z,\rho)$ and $K=B(\zeta,\varrho)$ closed balls, $B$ a proper subset of $K$ (you asked about $\subset$ in your post; in general it's ambiguous but here it definitely means proper subset, the theorem is clearly false if $K=B$). Clearly then, $\varrho>\rho$ (specifically $\varrho\ge\rho+d(z,\zeta)$ and if $z=\zeta$ then $\varrho>\rho$ is obvious). Note $K'=B(\zeta',\varrho)$ with $\zeta'=\zeta+\frac{1}{n}(y-x)$. Treat the case $B$ does not intersect $K$'s boundary i.e. $y$ is the centre $z$ of $B$. To obtain $B\subset K'$ we can be happy if we just have $\|z-\zeta'\|<\varrho-\rho$; observe in this case that $\varrho>\rho+d(z,\zeta)$ strictly (why?). Hint: $\|z-\zeta'\|$ is approximately $\|z-\zeta\|$ plus $\mathcal{O}(1/n)$ and we can arrange this to be suitably small. What about the case $B$ meets $K$'s boundary? Then you can argue that $y,z,\zeta$ are collinear and all triangle inequalities become exact equalities; that's my hint for the second bit.

For the claim that $K'$ can be arranged disjoint from $S$, an alternative to their sequence approach is to take a large segment of the ball $K$ not containing the intersection $x$, this segment covering at least the hemisphere opposite to $x$ plus a little more (more formally this is going to be the locus $K''=\{a\in K:\langle a-\zeta,x-\zeta\rangle<\delta\}$ for a fixed $0<\delta<\varrho^2$), use openness of the complement of $S$ and compactness of this locus to find some $\epsilon>0$ such that, for $a\in K''$, $a+t(a-\zeta)\notin S$ for all $0\le t\le\epsilon$, and then argue for sufficiently large $n$, at least so large that $\frac{1}{n}(y-x)<\epsilon$ but possibly larger, we have $K'\cap S=\emptyset$. The idea is that no intersections with $K''+\frac{1}{n}(y-x)\cap S$ could occur, and intersections with $K'\setminus K''$ are eventually impossible because such points would lie in the interior of $K$, so long as $n$ is large enough.

---

For the proof of the "$S$ is convex" theorem: the most important point is at the start; the claim that the possible radii are bounded is of course crucial for the argument but uses the nonconvexity hypothesis in an easily missed way. I earlier commented: "there must be something wrong with this proof, as it seems to show that if we take balls about any $z\notin S$ then we find a contradiction". But I was wrong (sorry), but the authors certainly could have emphasised this key idea a little more. Consider the following:

Here I start with a genuinely convex $S$ (which incidentally does not have this unique closest point property, but that's not the point) and some arbitrary $z_0$ outside of it. As you can see, it is in fact possible to make arbitrarily large balls about $z_0$ which don't touch $S$. It is extremely important to their proof that the point outside of $S$ is drawn from a "missing" point from a linear interpolation of points of $S$, because we would get some points "the other side" of $z_0$ belong to $S$ that would prevent me from making such a construction.

$S$ is obviously nonconvex in this example, but it demonstrates the point that if we have $z_0$ "sandwiched" between two points of $S$ then we are limited in how large our balls can be. As the largest ball shows, the fact we have a fixed $B(z,\rho)$ which all the other balls are forced to contain is also crucial! Else I could do something like this:

Where I have exploited the fact I'm allowed to let these balls only just barely contain $z_0$ to grow their radii arbitrarily large.

Enough pictures - let's formalise this: in the situation that $S$ is a closed set containing $a,b$ and $z=a+\lambda(b-a)$, $\lambda\in(0,1)$ does not lie in $S$, there is an upper limit on the radii of balls $B$ such that $B$ contains $B(z,\delta)$ for a fixed $\delta>0$ s.t. $B(z,\delta)\cap S=\emptyset$. Here $B(,)$ denotes closed balls. Suppose $B(x,\rho)$ contains $z$ and has interior disjoint from $S$. We may find some $n$ such that $v:=x-n$ is on the (infinitely extended) line that passes through $a,b,z$ and such that $n$ is orthogonal to $b-a$ i.e. orthogonal to the line. Specifically, $n$ is given by $x-a-\frac{(x-a)\cdot(b-a)}{\|b-a\|^2}(b-a)$. Note $z=v+w$ where $w$ is orthogonal to $n$ and $d(x,z)=\sqrt{\ell^2+\kappa^2}\le\rho$ where $\ell:=\|n\|,\kappa:=\|w\|$. Let $\eta$ be the maximum positive real such that both of $v\pm\eta\frac{(b-a)}{\|b-a\|}$ are in $B(x,\rho)$ (the maximum is clearly attained by closedness reasons and the fact neither $a$ nor $b$ can be in the interior of $B(x,\rho)$). We then in fact have $\rho^2=\ell^2+\eta^2$ and $\eta\ge\kappa$. The maximum $h$ such that $z-h\frac{n}{\|n\|}$ is in $B(x,\rho)$ satisfies $(\ell+h)^2+\kappa^2=\rho^2$ and it follows $0\le h\le\rho-\ell=\rho(1-\sqrt{1-\eta^2/\rho^2})=\mathcal{O}(\eta^2/\rho)$; observe furthermore that $z\in B(x,\rho)$ as well as both (two sidedness!) $d(x,a),d(x,b)\ge\rho$ forces $v\in[a,b]$ and thus $\eta\le\|b-a\|$ is bounded; we then see $\lim_{\rho\to\infty}h=0$. To elaborate, if $v=a+\mu(b-a)$ for $\mu<0$ strictly then $a\in[v,z]$ is in the interior of $B(x,\rho)$ as $d(x,a)=\sqrt{\ell^2+\mu^2\|b-a\|^2}<\sqrt{\ell^2+(\lambda-\mu)^2\|b-a\|^2}=d(x,z)\le\rho^2$, and similarly for the case $\mu>1$. The general Pythagorean principle is doing the heavy lifting here.

Therefore there is a bounding $\varrho$ so large that if $\rho\ge\varrho$ then $h<\delta$ and $B(x,\rho)$ cannot contain $B(z,\delta)$. Therefore the admissible radii are bounded!