How to squeeze the logistic function obliquely?

Question

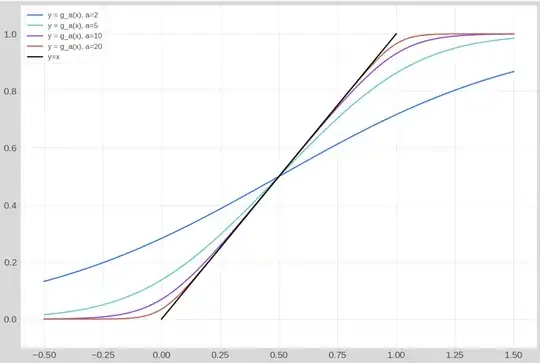
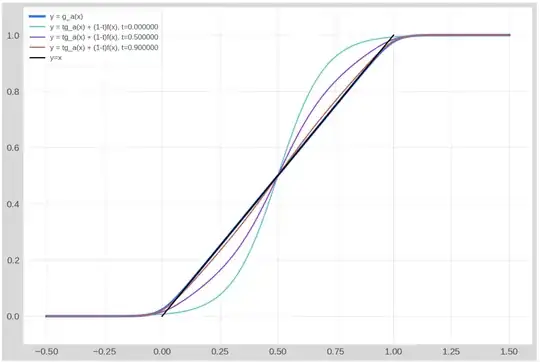
The original function: $f(x) = \frac{1}{1+e^{-10(x-0.5)}} $. Its graph (blue line) is shown here:

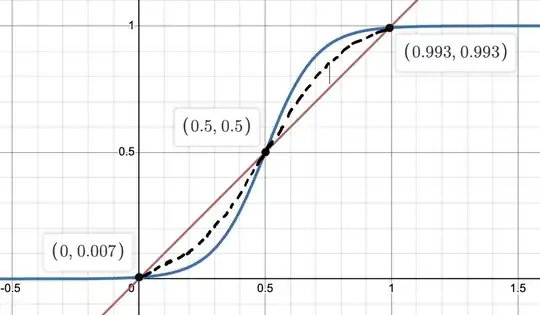
How can I squeeze this function obliquely along the $y=x$ line? The squeezed function $g$ needs to satisfy that $g(0.5) = 0.5$, $g(0)$ is close to $0$, and $g(1)$ is close to $1$. The graph of this function $g$ that I have in mind is the black line in the image above.

Answer 1

There are a few options here. You could simply take $g(x) = t x + (1-t) f(x)$ for $0 < t < 1$, but presumably you want $0 < g(x) < 1$ for all $x$. You could somehow define $g(x)$ piecewise, but this would not be smooth.

If you want a smooth function $g(x)$ with $0 < g(x) < 1$, $g(x) \approx 0$ for $x < 0$, $g(x) \approx 1$ for $x > 1$, and $g(x) \approx x$ for $0 < x < 1$, you can use $g_a(x) = L_a(x) - L_a(1-x) + 1-x$ where $L_a(x) = \frac{1}{a}\log(1 + \exp(ax))$ is the softplus and $a$ is a parameter that makes $g(x)$ closer to $x$ between $0$ and $1$.

If you want a function that looks closer to $f(x)$, you could try something like $y = tg_a(x) + (1-t) f(x)$, shown here for $a = 30$ and various $t$.