Why isn't the ∞-groupoidification of a category 1-truncated?

Question

I don't know how to reconcile the following facts:

• The nerve $N(\mathcal C)$ of a category is a 2-coskeletal simplicial set (source).
• An $n$-coskeletal Kan complex has trivial homotopy groups above degree $n-1$ (source).
• The geometric realisation of a category is a Kan fibrant replacement of its nerve (identifying Kan complexes with topological spaces for my purposes) (source).
• The Kan fibrant replacement of the nerve of a category has the same geometric realisation as the nerve, up to weak homotopy equivalence (source). In particular, it should have the same homotopy groups.
• Yet, every space arises as the geometric realisation of a category (even a poset). In particular, this MSE answer gives the poset displayed below as an example of a category whose geometric realisation is a sphere (and I have no trouble believing this).

So, I apologise for asking such a vague question, but intuition is completely failing me and I am very confused: how can the geometric realisation of a 1-category have higher homotopical information? Where does it come from? Is this related to model category theory, i.e. using 1-categories to model ∞-categories?

Answer 1

The mistake lies in combining the first two bullets to conclude that $N(\mathcal{C})$ has no nontrivial higher homotopy groups, because $N(\mathcal{C})$ is generally not a Kan complex*. On the other hand, a Kan fibrant replacement of $N(\mathcal{C})$ will generally not be $2$-coskeletal anymore. The rest of the bullets are all correct (the first two as well, for that matter), but since we have found we don't actually have any restrictions anymore on the higher homotopy groups of $N(\mathcal{C})$, you don't get a contradiction anymore.

*It is a Kan complex precisely if $\mathcal{C}$ is a groupoid. But in that case, $N(\mathcal{C})$ is a disjoint union of the nerves of connected components of $\mathcal{C}$, so let us assume for simplicity that $\mathcal{C}$ is connected. Then it is up to equivalence of categories a group, and hence $N(\mathcal{C})$ is a $K(G,1)$ for some group $G$. This indeed has no higher homotopy groups, so in those cases where our initial category $\mathcal{C}$ satisfies that $N(\mathcal{C})$ happens to be a Kan complex, it does hold that its geometric realization has no higher homotopy groups and we have no contradiction.

Answer 2

how can the geometric realisation of a 1-category have higher homotopical information?

This question hasn't really been addressed so let's talk about it. As Daniël says, this doesn't happen if the $1$-category is a groupoid. You refer to the geometric realization of the nerve as the $\infty$-groupoidification in the title, so I assume you know its universal property: $|N(C)|$, regarded as an $\infty$-groupoid, is the localization of $C$ (regarded as an $\infty$-category) where we invert all of its morphisms. If $C$ is already a groupoid then nothing needs to be inverted so it makes sense that we just get a $1$-groupoid in this case.

So, the higher homotopy must come from having to adjoin inverses of morphisms which are not already invertible in $C$. For every morphism $f : c \to d$ we adjoin a new morphism $f^{-1} : d \to c$ and some coherence $2$-morphisms $f^{-1} \circ f \cong \text{id}_d, f \circ f^{-1} \cong \text{id}_d$ witnessing the fact that $f^{-1}$ is an inverse of $f$, satisfying some coherences (the triangle identities) up to some higher coherences, etc. These coherences must be where the higher homotopy is coming from, so it must be the case that we can in general find some composite of higher coherences which is not required to be trivial.

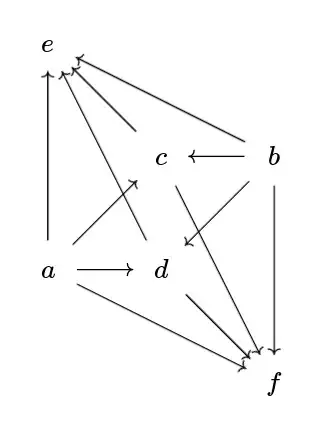
So let's use Eric Wofsey's very nice example of that $6$-element poset $P$ whose geometric realization $|N(P)|$ is (homotopy equivalent to) $S^2$, which I think must be a minimal example. The image you gave is really nice because you can really see the $2$-cell visually; let's try to see it in terms of coherences. Since there is a unique morphism in $P$ between any two objects I will just name that morphism using the name of the two objects, e.g. the unique morphism from $a$ to $e$ I will name $\overrightarrow{ae}$. So, observe that in the geometric realization we have two paths

$$\overrightarrow{af} \overrightarrow{ae}^{-1}, \overrightarrow{bf}\overrightarrow{be}^{-1} : e \to f$$

from the "north pole" to the "south pole," and these paths are homotopic ($S^2$ is simply connected) but there are two different homotopies between them, one of which goes "east" through $c$ (which involves writing $\overrightarrow{ae} = \overrightarrow{ce} \overrightarrow{ac}$ and $\overrightarrow{af} = \overrightarrow{cf} \overrightarrow{ac}$, then taking inverses, then applying an inverse coherence to $\overrightarrow{ac} \overrightarrow{ac}^{-1}$) and the other of which goes "west" through $d$ (similarly).

Having freely adjoined inverse coherences, there is no reason these two homotopies should themselves be homotopic! And the difference between them (traveling all the way around the "equator") ought to be a generator of $\pi_2(S^2)$. Of course I haven't proven this but you were asking a question about intuition and hopefully it is more intuitively plausible now.