Reminder: this uses the sign convention that vectors square to the opposite of the squared norms. Many sources use the opposite sign convention too. Here, $C\ell(p,q)$ is generated by $p$ sqrts of $-1$ and $q$ sqrts of $+1$, all anticommuting. Note $C\ell(k,0)=C_k$ and $C\ell(0,k)=C_k'$ in OP's notation.
You remember the classification of Clifford algebras with the Clifford clock:
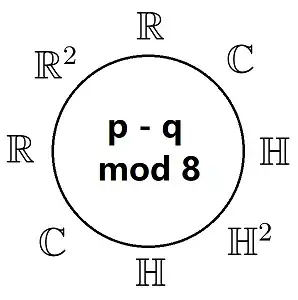
The signature $p-q$ mod $8$ starts at $0$ at the top. It is easy enough to remember the first three, since $\mathbb{R},\mathbb{C},\mathbb{H}$ are respectively generated by $0,1,2$ roots of $-1$. From there on, the Clifford algebra $C\ell(p,q)$ is isomorphic to $\mathbb{K}(2^k)$, where the notation $\mathbb{K}(m)$ means the $m\times m$ matrix algebra over $\mathbb{K}$, and here you look up $\mathbb{K}\in\{\mathbb{R},\mathbb{R}^2,\mathbb{C},\mathbb{H},\mathbb{H}^2\}$ from the Clifford clock. You can solve for $k$ in $C\ell(p,q)\cong\mathbb{K}(2^k)$ by equating dimensions: the left side has dimension $2^n$ (where $n=p+q$) and the right side has real dimension $(\dim_{\mathbb{R}}\mathbb{K})\cdot 2^{2k}$.
Notice the symmetry across the diagonal between $-1,3$ mod $8$. And the antisymmetry across the other diagonal. So once you know the first three, and the antisymmetry, you just need to remember $\mathbb{H}^2$. You should also have the corner $C\ell(p,q)$ for $p+q\le 2$ of the table memorized if you understand split complex numbers and split quaternions.
The symmetry is offset by $1$ from the "nicer" horizontal symmetry because the even Clifford subalgebra is $C\ell_0(p,q)\cong C\ell(p-1,q)$. This is perhaps even more illuminated in the super algebra setting.
