4

$$\int_1^e\sqrt{\ln x}\;\mathrm{d}x$$

WolframAlpha provides an answer to the integral in terms of the imaginary error function. However, I was wondering why the method I employed did not work:

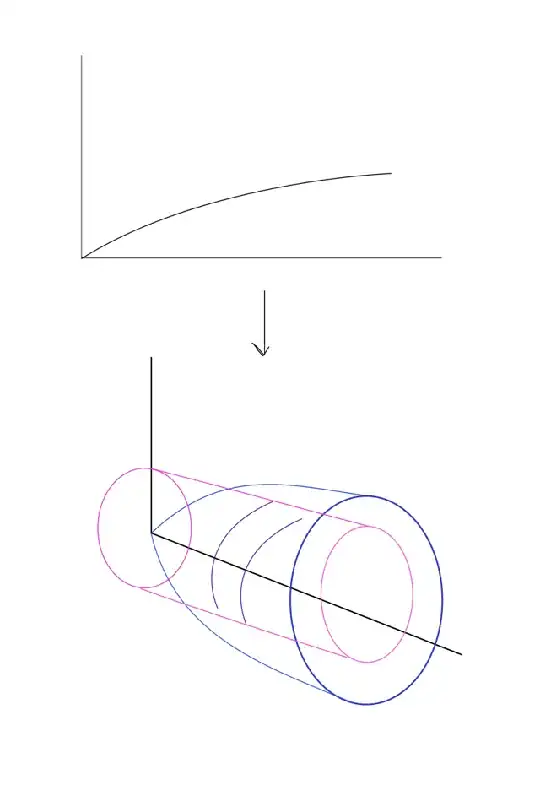
I can construct a solid formed by rotating $\sqrt{\ln x} \,\,(1\leq x\leq e)$ around the $x$-axis, whose volume is given by $\pi\displaystyle\int_1^e \big(\sqrt{\ln x}\big)^2dx$, which is equal to $\pi$. I can compare this volume to that of a cylinder with height $e-1$, and I solve for the radius which can used to find half the cross-sectional area. $\pi r^2(e-1)=\pi\implies r=\frac{1}{\sqrt{e-1}}$, and half the area of the cross-sectional area is $r\cdot(e-1)=\color{blue}{\sqrt{e-1}}$. And my picture (below) should imply that the cross-sectional area is equal to the integral, right?

Cylinder-Logarithm

I believe my thoughts were somewhat along the lines of Cavalieri's principle, but I can't exactly formulate the words. Obviously, my method is wrong here (by WolframAlpha), so I would like to know where my mistake exactly is, and another way of solving the integral.

Travis Willse
  • 108,056
sreysus
  • 797
  • 3
    Why should the area of the cross-section be determined by the cross-section of the cylinder? In general, there is no way to determine $\int f(x); dx$ from $\int f(x)^2; dx$. – Robert Israel Dec 29 '23 at 18:06
  • I think the following better explains my thinking: Every cylinder can be uniquely determined by its height and the radius of its circle. I fixed the height, and if the volume of the cylinder is equal to the volume of the solid, then the radius must have a fixed value that can be obtained by setting the volumes equal to each other (like I did in the post). Then, the radius times the height of the cylinder should be equal to the actual integral, right? I know that determining $\int f(x)dx$ from $\int f(x)^2dx$ sounds too good to be true, but I just want to know where the flaw is in my argument. – sreysus Dec 29 '23 at 18:26
  • 1
    Wrong, the radius times the height of the cylinder is not the cross-sectional area of the solid. – Robert Israel Dec 29 '23 at 19:13
  • So, (also with the understanding of @TravisWillse's counterexample) although the radius times the height is equal to half the cross-sectional area of the $\color{blue}{\mathrm{cylinder}}$, this does not imply that the product is equal to the cross-sectional area of the $\color{blue}{\mathrm{solid}}$ formed by rotating $\sqrt{\ln x}$. I also found a picture in my head that helps explain this. I still feel that this is a bit awkward, but I get why I'm wrong. Thanks! – sreysus Dec 29 '23 at 19:24

2 Answers2

2

In general the (signed) cross-sectional area cannot be determined from the volume of the solid of revolution it generates, that is, the definite integral $\int_a^b f \,dx$ cannot in general be determined from $\int_a^b f^2 \,dx$.

For example, the functions $f(x) := \sqrt 3 x$ and $g(x) = 1$ satisfy (over the interval $[a, b] = [0, 1]$) $$\int_0^1 f^2 \,dx = 1 = \int_0^1 g^2 \,dx$$ but $$\int_0^1 f \,dx = \frac{\sqrt 3}2 \qquad \textrm{and} \qquad \int_0^1 g \,dx = 1.$$

As for the integral itself, substituting $x = e^{y^2}$ yields $$\int_1^e \sqrt{\ln x} \,dx = 2 \int_0^1 y^2 e^{y^2} \,du ,$$ and integrating by parts with $u = y$, $dv = 2 y e^{y^2}$ gives $$\left.y e^{y^2}\right\vert_0^1 - \int_0^1 e^{u^2} \,du = e - \int_0^1 e^{u^2} \,du.$$ The integrand $e^{u^2}$ does not have an antiderivative expressible in closed form in terms of terms of elementary functions, but in terms of the purpose-built imaginary error function, $$\operatorname{erfi} x := -i \operatorname{erf} ix = \frac2{\sqrt \pi} \int_0^x e^{u^2} \,du,$$ we have $$\int_1^e \sqrt{\ln x} \,dx = e - \frac{\sqrt \pi}2 \operatorname{erfi} 1 = 1.25563\ldots .$$

Travis Willse
  • 108,056
2

Another approach for getting the answer without referring directly to special functions...

$$\int_{1}^{e}\sqrt{\ln(x)}\space dx = \int_{0}^{1}e^u\sqrt{u}\space du$$

$$=\sum_{k=0}^{\infty}\frac{1}{k!} \int_{0}^{1}u^{k+\frac{1}{2}}\space du$$

$$=\sum_{k=0}^{\infty}\frac{1}{k!(k+\frac{3}{2})} \approx 1.25563 $$

Volk
  • 2,740
  • 1
  • 4
  • 13