1

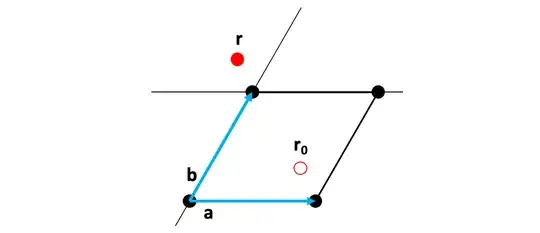
move a point back into the unit cell

Given a 2D lattice defined by vectors $\mathbf{a}, \mathbf{b}$ and a point $\mathbf{r}$ how to find the corresponding point $\mathbf{r_0}$ in the original unit cell defined by the two vectors?

Something simple like

$$\mathbf{r_0} = \mod((\mathbf{a} \cdot \mathbf{r}), 1) \ \mathbf{a} \ \ + \mod((\mathbf{b} \cdot \mathbf{r}), 1) \ \mathbf{b}$$

does not seem to work.

update: While I'm asking for a general solution (in 2D) I'll be testing it first on a hexagonal lattice with $\mathbf{a}, \mathbf{b} = (1, 0), (1/2, \sqrt{3}/2)$ and $\mathbf{r} = (0, 1)$.

uhoh
  • 1,967
  • 1
    You'll want to start by writing $r$ as a linear combination of $a$ and $b$. Are you familiar with change of basis? – TomKern Dec 19 '23 at 02:09
  • @TomKern the "idea" of it, yes; the practice, not in several decades :-) I suppose that's what I was trying to do with those dot products in the question. My guess is that there's a matrix to do it, and perhaps I've only got two out of the four elements so far. I'm aware that this is not a hard question and frustrated that the solution isn't simply obvious to me. – uhoh Dec 19 '23 at 02:36

3 Answers3

1

Note that $\bf{a}$ and $\bf{b}-\displaystyle\frac{(\bf{b}\cdot\bf{a})}{\lvert\bf{a}\rvert^2}\bf{a}$ is a orthogonal basis for the $2D$ lattice. Thus, $$\bf{r}_0=\alpha\bf{a}+\beta\left(\bf{b}-\displaystyle\frac{(\bf{b}\cdot\bf{a})}{\lvert\bf{a}\rvert^2}\bf{a}\right),$$ where it is not hard to show that $$\alpha=\frac{\left(\bf{a}\cdot\bf{r}_0\right)}{\lvert\bf{a}\rvert^2} \ \ \text{and} \ \ \beta=\frac{1}{\left|\bf{b}-\displaystyle\frac{(\bf{b}\cdot\bf{a})}{\lvert\bf{a}\rvert^2}\bf{a}\right|^2}\left[\bf{r}_0\cdot\left(\bf{b}-\displaystyle\frac{(\bf{b}\cdot\bf{a})}{\lvert\bf{a}\rvert^2}\bf{a}\right)\right].$$

QuantumSuperfield
  • 2,751
  • I think that the idea here is to get $r_0$ by applying modulo 1 to $\alpha$ and $\beta$ obtained from $\mathbf{r}$, but so far I'm still struggling with this orthogonal basis. If I start with a simple hexagonal lattice $\mathbf{a}, \mathbf{b} =(0, 1), \ (1/2, \sqrt{3}/2)$ and the point $\mathbf{r} = (0, 1)$, I get $\alpha, \beta = 0, \ 2/\sqrt{3}$. Now $\alpha \ \mathbf{a} = (0, 0)$, but $$\beta \ \left(\mathbf{b} - \frac{\mathbf{b} \cdot\mathbf{a}}{|\mathbf{a}|^2} \mathbf{a} \right) = (1/\sqrt{3}, \ 1) \ne \mathbf{r_0}.$$ So I'm currently stuck. – uhoh Dec 19 '23 at 00:36
  • I've added this example back into the question. – uhoh Dec 19 '23 at 00:52
1

We're trying to find $m$ and $n$ such that $\mathbf{r}$ is $m\mathbf{a}+n\mathbf{b}$, which is the result of multiplying the matrix $\begin{pmatrix}a_1 & b_1 \\ a_2 & b_2 \end{pmatrix}$ by $\begin{pmatrix}m\\n\end{pmatrix}$. If you multiply a matrix $M$ by a vector $\mathbf{v}$, it's just the first component of $\mathbf{v}$ times the first column of $M$ plus the second component of $\mathbf{v}$ times the second column of $M$ etc.

So, if: $$\mathbf{r} = \begin{pmatrix}a_1 & b_1 \\ a_2 & b_2 \end{pmatrix} \cdot \begin{pmatrix}m\\n\end{pmatrix}$$ Then: $$\begin{pmatrix}a_1 & b_1 \\ a_2 & b_2 \end{pmatrix}^{-1} \cdot \mathbf{r} = \begin{pmatrix}m\\n\end{pmatrix}$$ $$\frac{1}{a_1 b_2 - b_1 a_2} \begin{pmatrix}b_2 & -b_1 \\ -a_2 & a_1 \end{pmatrix} \cdot \mathbf{r} = \begin{pmatrix}m\\n\end{pmatrix}$$

Use this to solve for $m$ and $n$, then take their fractional parts (mod 1), then plug them back into $m\mathbf{a}+n\mathbf{b}$.

TomKern
  • 3,407
  • Oh! I knew I wanted to divide $r$ by $\mathbf{a}$ and $\mathbf{b}$ somehow, but the reciprocal vectors didn't make sense. Now I see I should have "dotted" $\mathbf{r}$ with the inverse, not the reciprocal. Thanks! (I'm guessing that this works in higher dimensions, using the appropriate method to find the inverse) – uhoh Dec 19 '23 at 06:41
1

The general solution to this problem is of importance to crystalline physics and it is known as reciprocal vectors.

It is pretty easy to understand. You have $\vec a$ and $\vec b$ making your 2D lattice. Create new vectors $\vec c$ and $\vec d$ with the property that $\vec c\cdot\vec b=0=\vec d\cdot\vec a$ and then $\vec a\cdot\vec c=1=\vec b\cdot\vec d$. Then, with whatever initially given vector $\vec r$, you can decompose it as $\vec r=(\vec r\cdot\vec c)\,\vec a+(\vec r\cdot\vec d)\,\vec b$ so that you can do your modulo operation on those coefficients and get the answer.

In crystalline physics, we usually use reciprocal lattice vectors with a slightly different definition, because we care more about parametrising the Brillouin zone. The topic is also connected with the metric and its inverse; you do not actually have to compute those vectors $\vec c$ and $\vec d$ directly if you just want this decomposition. Still, for your current purpose, this is the easiest thing to do.

You had better take care about whether you want results in $[0,1)$ or in $(-\frac12,+\frac12]$. Your expansion is wrong; the answer is really $(.42265,0.1547)$

naturallyInconsistent
  • 297