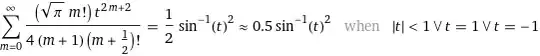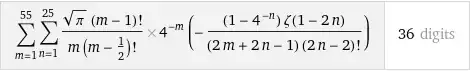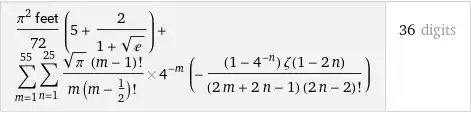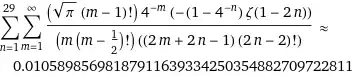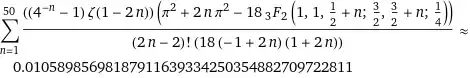An idea for this difficult integral: $\int_{-\tfrac{1}{2}}^{\tfrac{1}{2}}\dfrac{\arccos x}{\sqrt{1-x^2}(1+e^{-x})}dx$.

Question

I am being stuck in caculating this integral: $$J=\int_{-\tfrac{1}{2}}^{\tfrac{1}{2}}\dfrac{\arccos x}{\sqrt{1-x^2}(1+e^{-x})}dx$$ I tried to change to another variable: $x = - t$ then $dx = - dt$, also I got: $$J=\int_{-\tfrac{1}{2}}^{\tfrac{1}{2}}\dfrac{\arccos(-t)}{\sqrt{1-t^2}(1+e^t)}dt=\int_{-\tfrac{1}{2}}^{\tfrac{1}{2}}\dfrac{\arccos(-x)}{\sqrt{1-x^2}(1+e^x)}dx.$$ Therefore $$2J=\int_{-\tfrac{1}{2}}^{\tfrac{1}{2}}\left[\dfrac{\arccos x}{\sqrt{1-x^2}(1+e^{-x})}+\dfrac{\arccos(-x)}{\sqrt{1-x^2}(1+e^x)}\right]dx=\int_{-\tfrac{1}{2}}^{\tfrac{1}{2}}\dfrac{e^x\arccos x+\arccos(-x)}{\sqrt{1-x^2}(1+e^x)}dx$$ The numerator looks very complex and I really do not know how to do next. Can you guys give me some ideas ?

Answer 1

A partial approach.

Using $x=\cos(t)$ you can prove that $$J=\int_{\frac \pi 3}^{\frac {2\pi} 3}\frac{t}{1+e^{-\cos (t)}}\,dt$$ and notice that, for the range of integration $\frac{1}{1+e^{-\cos (t)}}$ is close to linearity.

Using series built around the mid point of the interval of integration $$\frac{1}{1+e^{-\cos (t)}}=\frac 12+\frac 14\sum_{n=0}^\infty (-1)^{n+1}\,a_n\, \left(t-\frac{\pi }{2}\right)^{2 n+1} $$

So $$J=\frac{\pi ^2}{12}+\frac {\pi^3}{432}\sum_{n=0}^\infty (-1)^{n+1}\,a_n\, \frac{\pi ^{2 n}}{(2 n+3)\,36^n}$$

The problem is that the coefficients $a_n$ $$\left\{1,\frac{1}{4},\frac{7}{120},\frac{49}{2880}, \frac{353}{72576},\frac{3377}{2419200}, \frac{2505427}{6227020800}\,\cdots\right\}$$ do not seem to correspond to any known sequence in $OEIS$.

But the convergence is quite fast. Using partial sums and converting to decimals $$\left( \begin{array}{cc} p & J_{(p)} \\ 0 & 0.798542437220 \\ 1 & 0.799526296803 \\ 2 & 0.799481341688 \\ 3 & 0.799484137569 \\ 4 & 0.799483958284 \\ 5 & 0.799483970221 \\ 6 & 0.799483969403 \\ 7 & 0.799483969460 \\ 8 & 0.799483969456 \\ \end{array} \right)$$

Edit

Another possibility is to write $$\frac{1}{1+e^{-\cos (t)}}=\frac 12-\frac 12 \sum _{n=0}^{\infty }\frac{E_{2 n+1}(0)}{ (2 n+1)!} \,\cos ^{2n+1}(t)$$ and use $$\int_{\frac \pi 3}^{\frac {2\pi} 3} t\,\cos ^{2n+1}(t)\,dt=\frac {A_n} {3\times 4^{n+2} \,(n+1)\, (2 n+3) }$$ with $$A_n=6 \, _3F_2\left(1,n+\frac{3}{2},n+\frac{3}{2};n+2,n+\frac{5}{2};\frac{1}{4}\right)-$$ $$\sqrt{3} \pi (2 n+3) \, _2F_1\left(1,n+\frac{3}{2};n+2;\frac{1}{4}\right) $$

If $B_n$ is the summand, an approximation is $$\frac {B_{n+1}}{B_n}=-\frac{1}{40}\Bigg(1-\frac{1}{n}+\frac{2}{n^2}+O\left(\frac{1} {n^3}\right)\Bigg)$$

Computing the partial sums and converting to decimals $$\left( \begin{array}{cc} p & J_{(p)} \\ 0 & 0.822467033424 \\ 1 & 0.799191953953 \\ 2 & 0.799489239013 \\ 3 & 0.799483865054 \\ 4 & 0.799483971630 \\ 5 & 0.799483969410 \\ 6 & 0.799483969457 \\ 7 & 0.799483969456 \\ \end{array} \right)$$

Using this for, we have a very fast convergence : looking at the absolute error $$\log(\Delta_p) \sim -3.77\, p-8.62$$ while for the first one it was $$\log(\Delta_p) \sim -1.37\, p-5.10$$

Update

We could also use $$\int_{\frac \pi 3}^{\frac {2\pi} 3} t\,\cos ^{2n+1}(t)\,dt=-\int_{-\frac \pi 6}^{+\frac {\pi} 6} \left(x+\frac{\pi }{2}\right) \sin ^{2n+1}(x)\,dx=$$ $$-\frac{1}{6} \pi B_{\frac{1}{4}}\left(n+1,\frac{1}{2}\right)+$$ $$\frac{2^{-(2 n+3)}}{(n+1) (2 n+3)}\, _3F_2\left(1,n+\frac{3}{2},n+\frac{3 }{2};n+2,n+\frac{5}{2};\frac{1}{4}\right)$$ and obtain slightly better results $$\left( \begin{array}{cc} p & J_{(p)} \\ 0 & 0.799191953953 \\ 1 & 0.799489239013 \\ 2 & 0.799483865054 \\ 3 & 0.799483971630 \\ 4 & 0.799483969410 \\ 5 & 0.799483969457 \\ 6 & 0.799483969456 \\ \end{array} \right)$$

Answer 2

Let us try to get the solution in the form of series.

$\color{brown}{\textbf{Primary Transformation,}}$

Firstly, $$I=\int\limits_{\large-\frac12}^{\large\frac12}\dfrac{\arccos(x)\,\text dx}{\sqrt{1-x^2}\left(1+e^{-x}\right)} =\int\limits_{\large-\frac12}^{0}\frac{\arccos x\,\text dx}{\sqrt{1-x^2}\left(1+e^{-x}\right)} +\int\limits_{0}^{\large\frac12}\frac{\arccos x\,\text dx}{\sqrt{1-x^2}\left(1+e^{-x}\right)}$$ $$=\int\limits_0^{\large\frac12}\frac{\pi\,\text dx}{\sqrt{1-x^2}\left(1+e^{x}\right)} -\int\limits_{0}^{\large\frac12}\frac{\arccos x\,\text dx}{\sqrt{1-x^2}\left(1+e^{x}\right)} +\int\limits_{0}^{\large\frac12}\frac{\arccos x}{\sqrt{1-x^2}}\dfrac{e^{x}\,\text dx}{1+e^{x}}$$ $$=\int\limits_0^{\large\frac12}\frac{\pi-2\arccos x}{\sqrt{1-x^2}} \dfrac{\,\text dx}{1+e^{x}} +\int\limits_{0}^{\large\frac12}\dfrac{\arccos x}{\sqrt{1-x^2}}\,\text dx$$ $$=\int\limits_0^{\large\frac12}\frac{2\arcsin x}{\sqrt{1-x^2}} \dfrac{\text dx}{1+e^x} +\frac12{\arccos^2 x}\bigg|_0^{\large\frac12} =\int\limits_0^{\large\frac12} \dfrac{\text d\left(\arcsin^2 x\right)}{1+e^x}+\frac5{72}\pi^2$$ $$=\frac5{72}\pi^2+\dfrac{\arcsin^2 x}{1+e^x}\bigg|_0^{\large\frac12} +\int\limits_0^{\large\frac12} \left(\arcsin^2 x\right)\dfrac{e^x\,\text dx}{\left(1+e^x\right)^2},$$ $$I=\frac5{72}\pi^2+\dfrac{\pi^2}{36\left(1+\sqrt e\right)}+I_1,\tag1$$ where $$I_1=\int\limits_0^{\large\frac12} \left(\arcsin^2 x\right) \dfrac{e^x\,\text dx}{\left(1+e^x\right)^2}.\tag2$$

$\color{brown}{\textbf{The square of arcsinus.}}$

From the known series $$\arcsin s=t+\dfrac{1}{2}\,\dfrac{t^3}3+\dfrac{1\cdot3}{2\cdot4}\,\dfrac{t^5}5+\dfrac{1\cdot3\cdot5}{2\cdot4\cdot6}\,\dfrac{t^7}7 +\dfrac{1\cdot3\cdot5\cdot7}{2\cdot4\cdot6\cdot8}\,\dfrac{t^9}9 +\dfrac{1\cdot3\cdot5\cdot7\cdot9}{2\cdot4\cdot6\cdot8\cdot{10}}\, \dfrac{t^{11}}{11}+\dots$$

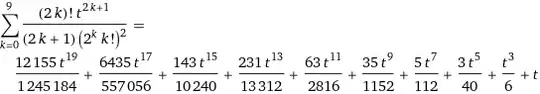
can be obtained series for its square in the form of $$h(t)=\frac12 \arcsin^2(t) =\sum\limits_{m=1}^\infty H_{2m}\, t^{2m},\quad H_{2m}=\dfrac{\sqrt\pi\, (m-1)!}{(4m)\left(m-\frac12\right)!},\tag3$$ $$h(t)=\frac{t^2}2+\frac{t^4}{6}+\frac{4t^6}{45} +\frac{2t^8}{35}+\dfrac{64t^{10}}{1575}+\dfrac{64 t^{12}}{2079}+\dfrac{512 t^{14}}{21021}+\dfrac{128t^{16}}{6435}+\dfrac{16384 t^{18}}{984555}+\dots,$$

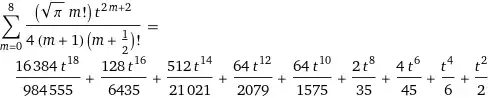
$\color{brown}{\textbf{The main integtal.}}$

From $(2-3)$ should $$I_1=\sum\limits_{m=1}^\infty H_{2m}\,J_{2m},\quad\text{where}\quad J_{2m} = \int\limits_0^{\large\frac12}\,\dfrac{e^{-x}}{(1+e^{-x})^2}\,x^{2m}\,\text dx.\tag4$$

Let $\,x=2y,\;$ then, taking in accountt the series $$\tanh(t)=\sum\limits_{n=1}^\infty\dfrac{ (16^n-4^n)\,\zeta(1-2n)}{(2n-1)!}\, t^{2n-1},\tag5$$ one can get $$J_{2m}=2^{2m+1}\int\limits_0^{\large\frac14}\frac{e^{2y}}{(1+e^{2y})^2}\,y^{2m}\,\text dy =2^{2m-1}\int\limits_0^{\large\frac14} y^{2m}\,\frac{\text dy}{\cosh^2(y)} =2^{2m-1}\int\limits_0^{\large\frac14} y^{2m}\,\text d(\tanh y)$$ $$=2^{2m-1} y^{2m}\tanh y\bigg|_0^{\large\frac14} - 2^{2m}\,m\,\int\limits_0^{\large\frac14} y^{2m-1}\tanh y,\text dy $$ $$=\frac12\,\frac{\sqrt e -1}{\sqrt e +1} 4^{-m} + 2^{2m}\,m\, \int\limits_0^{\large\frac14} y^{2m-1}\left(\sum\limits_{n=1}^\infty (16^n-4^n)\,\zeta(1-2n)\,\dfrac{y^{2n-1}}{(2n-1)!}\right),\text dy $$ $$=\frac12\,\frac{\sqrt e -1}{\sqrt e +1}\,4^{-m} + 2^{2m}\,m\, \left(\sum\limits_{n=1}^\infty\dfrac{ (16^n-4^n)\,\zeta(1-2n)}{(2m+2n-1) 4^{2m+2n-1}(2n-1)!}\right)$$ $$=4^{-m}\left(\frac12\,\frac{\sqrt e -1}{\sqrt e +1} + 4 m\, \sum\limits_{n=1}^\infty\dfrac{ (1-4^{-n})\zeta(1-2n)}{(2m+2n-1)(2n-1)!}\right)$$ $$=4^{-m}\left(\frac12\frac{\sqrt e -1}{\sqrt e +1} + 2\sum\limits_{n=1}^\infty\dfrac{(1-4^{-n})\zeta(1-2n)}{(2n-2)!}\left(\frac 1{2n-1}-\frac 1{2m+2n-1})\right)\right),$$ $$J_m=4^{-m}(J_{10} + J_{1m}),\tag6$$ where $$J_{10}=\frac12\frac{\sqrt e -1}{\sqrt e + 1} + 2\sum\limits_{n=1}^\infty \dfrac{(1-4^{-n})\zeta(1-2n)}{(2n-1)!}$$ $$=-\frac12\tanh\left(\frac14\right)+\frac12\frac{\sqrt e -1}{\sqrt e + 1}=0,$$ $$J_{1m} = 2\sum\limits_{n=1}^\infty \dfrac{(1-4^{-n})\zeta(1-2n)}{(2m+2n-1)(2n-2)!}$$

and $\;2D-$series

provide results $$I_1\approx \color{brown}{0.0105898569818791163933425035488270972},$$ and $$I\approx \color{brown}{0.7994839694564289116511716087564179}$$ (all digits are correct)

Besides, the change of the summation order a[[ows to use the infinity limit in the inner summation:

At last, can be presented $1D-$series in the form of