0

I am trying to better understand the visual interpretation of a Line Integral.

We are all told that a classic integral of a function represents the area under that function between two certain points - but I am trying to now extend this this visual to a line integral.

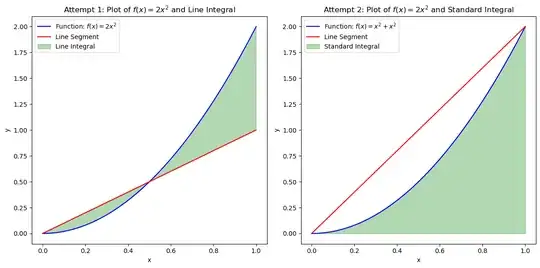
For example, suppose I want to integrate the function $f(x) = 2x^2$ over the line segment $(0,0)$ and $(1,1)$.

Intuitively, without trying to evaluate the line integral, here is my attempts to represent the line integral (Python code):

  import matplotlib.pyplot as plt
import numpy as np

def f1(x):
    return 2x*2


def f2(x):
    return x2 + x2


x = np.linspace(0, 1, 100)


y1 = f1(x)
y2 = f2(x)


x_line = np.array([0, 1])
y_line1 = np.array([0, 1])
y_line2 = np.array([0, 2])


fig, axs = plt.subplots(1, 2, figsize=(12, 6))


Attempt 1


axs[0].plot(x, y1, label='Function: $f(x) = 2x^2$', color='blue')
axs[0].plot(x_line, y_line1, label='Line Segment', color='red')


y_line_interp1 = np.interp(x, x_line, y_line1)


Shade the area between the blue curve and the red line


axs[0].fill_between(x, y1, y_line_interp1, where=(y1 >= y_line_interp1), color='green', alpha=0.3)
axs[0].fill_between(x, y1, y_line_interp1, where=(y1 <= y_line_interp1), color='green', alpha=0.3, label='Line Integral')


axs[0].set_xlabel('x')
axs[0].set_ylabel('y')
axs[0].set_title('Attempt 1: Plot of $f(x) = 2x^2$ and Line Integral')
axs[0].legend()


Attempt 2


axs[1].plot(x, y2, label='Function: $f(x) = x^2 + x^2$', color='blue')
axs[1].plot(x_line, y_line2, label='Line Segment', color='red')


Shade the area under the curve


axs[1].fill_between(x, y2, color='green', alpha=0.3, label='Standard Integral')


axs[1].set_xlabel('x')
axs[1].set_ylabel('y')
axs[1].set_title('Attempt 2: Plot of $f(x) = 2x^2$ and Standard Integral')
axs[1].legend()


plt.tight_layout()
plt.show()

enter image description here

My Question: I think Attempt 1 corresponds to the Line Integral whereas Attempt 2 corresponds to the Classic Integral. Have I correctly identified the area corresponding to the Line Integral?

Thanks!

UPDATE: As per the comments from @Anton Vrdoljak, the titles on both graphs have now been changed. As such, they should now be correct (?)

RobPratt
  • 50,938
stats_noob
  • 4,107
  • 1
    Perhaps you have to swap titles for your plots. – Anton Vrdoljak Dec 07 '23 at 17:04
  • Usually a line integral is defined over a multivariable function $f:\mathbb{R}^n\to\mathbb{R}^n$. In $\mathbb{R}^2$ it's intuitive, because it's the area underneath the graph and a certain curve $\gamma$. The line integral in $\mathbb{R}$ is just the regular definite integral. – Francesco Sollazzi Dec 07 '23 at 17:23
  • Have you seen L.Vieira's animation on Wikipedia? – user170231 Dec 07 '23 at 18:29
  • @ Anton Vrdoljak: thank you! i will do this right now! – stats_noob Dec 07 '23 at 22:21
  • @ user170231: thank you for your reply! I saw this animation but it was a bit too complicated for me to follow ... I wanted to make a simpler visualization to help me understand. thank you so much! – stats_noob Dec 09 '23 at 00:07
  • “We are all told that a classic integral of a function represents the area under that function between two certain points” well that is only one possible interpretation and it isn’t always the best one. Not everything is about areas/volumes (for line integrals you can try to relate it to areas under some curve but doesn’t mean you should). See here for similar remarks. Besides, what you have currently written doesn’t make sense; you can’t integrate a function from reals to reals over a line segment in the plane. – peek-a-boo Dec 09 '23 at 00:30
  • @ peek-a-boo: thank you so much for your reply! I will read the link you have posted for more information. – stats_noob Dec 09 '23 at 00:32

0 Answers0