Radius of circle given horizontal distances of two points and angle between them

Question

Problem

I'm not certain this is possible to solve (and indeed, if the answer is "don't be silly, that's not possible" then at the very least it'll save me some time!).

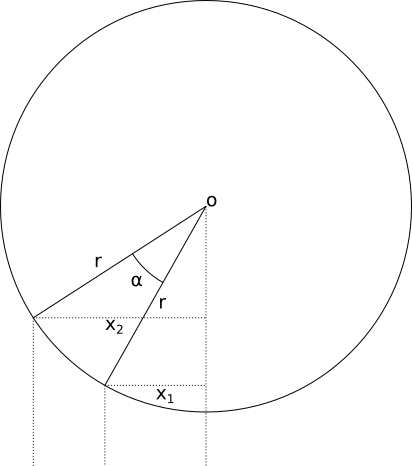
I am attempting to find the radius $r$ of a circle on which I know the horizontal position of two points (relative to the center), $x_1$ and $x_2$, and the angle between them, $\alpha$. I realize this certainly won't be possible in all cases, e.g. when $\alpha$ is zero or any multiple of $2\pi$ then there's a single point and no possible solution, but I'm not sure it's possible even if $\alpha$ is not these things.

Put simply: I know $x_1$, $x_2$, and $\alpha$. I need to find $r$.

Things I've tried so far: using the Cosine rule on the isosceles $\triangle{{x_1}{x_2}O}$ to produce an equation for the base (${x_1}\to{x_2}$) in terms of $r$ and $\alpha$, but of course while I know $\alpha$ I don't know the length of the base because I've only got the horizontal coordinates. Combining that with right-angle triangles dropped from $O$ proved fruitless, but perhaps I'm missing something here? Some searching on this site turned up numerous problems involving two points and a circle, but the closest I could find to my particular situation was "calculating the radius of a circle if the distance between two points and the angle from the center are known", but of course in this case I don't know the distance between these points, precisely.

Context

A couple of years ago, I was watching Matt Parker put a ludicrous number of RGB LEDs on his Christmas tree. Being in possession of a similarly ludicrous number of RGB LEDs, and a micro-controller needed to drive them (plus some small skill in coding on Raspberry Pis, and their cameras), I decided I should attempt something similar with ours. I got the micro-controller, and the LEDs, and even a nice web interface going. However, the calibration of the 3D positions of the LEDs on the tree proved too much to do in my spare time that year.

This year, I'm revisiting the problem. I've got to the point of a nice chunk of code (with web interface) that'll capture an image of the base tree (unlit), and an image of each LED lit in turn, at a series of arbitrary angles (specified by the user), calculating the positions of each LED as seen by the camera by diff'ing each capture to the (unlit) base capture.

Hence, in the diagram above, $O$ is looking down the trunk of the tree. I can estimate (pretty accurately) its location based on an average of the horizontal positions of all LEDs found in the captured images. $x_1$ and $x_2$ are the horizontal positions of a single LED captured at two different tree angles, and we know $\alpha$ because it's literally input from the user ("how far did you turn the tree?"). Calculating the radius $r$ will give me the distance of the LED from the trunk. We only have the horizontal positions because the diagram above is us looking at the tree down its trunk. The camera in this case is placed in "front" of the tree, hence why I've extended the dotted lines down below the diagram towards the "camera" (and yes, I realize they're not technically parallel in practice, but "good enough" is fine here!).

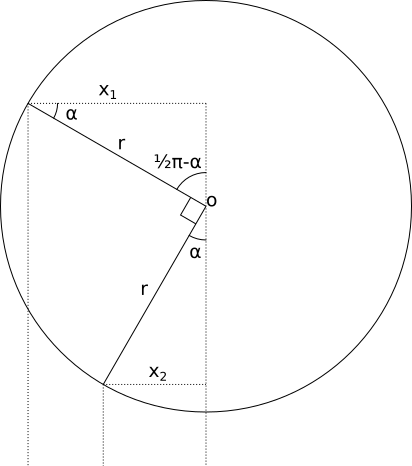
I did note that, though Matt doesn't go through his method of calibrating the positions of the LEDs (only the corrections post-calibration), he does mention that he rotated the tree through 90 degrees each time. This makes the problem much simpler:

If the tree is always rotated through a right-angle, we can take advantage of the congruence of two right-angled triangles and note that:

$$x_1 = r\cos{\alpha}\\ x_2 = r\sin{\alpha}\\ \frac{x_2}{x_1} = \frac{r\sin{\alpha}}{r\cos{\alpha}} = \tan{\alpha}\\ \alpha = \arctan{\frac{x_2}{x_1}}\\ r = \frac{x_1}{\cos{\alpha}} $$

Job done! But that gives you a maximum of four possible positions of the tree, and it can be quite fiddly to reach one of those positions in our diminutive living room with all the LEDs hooked up. Hence, I'd really like to be able to have the user specify arbitrary rotations of the tree and capture whatever happens to be convenient / necessary for reasonable calibration of the points. Unfortunately, my trigonometric knowledge has been steadily gathering dust for 30 years, and something in my gut is mumbling that there's not enough data to solve this; that a hack like forcing the rotation to be right-angles is required.

Am I barking up the wrong (Christmas) tree? Or just plain barking? I look forward to any (LED) light that you can shed! Alright, that's enough puns ...

Answer 1

Let $\beta$ be the angle opposite x1.

Initially we have:
$r = x_1/(\sin \beta)$
$r = x_2/\sin (\alpha +\beta)$

$\rightarrow x_1/(\sin \beta) = x_2/(\sin (\alpha +\beta)$
$\rightarrow x_2/x_1 = \sin (\alpha +\beta)/(\sin \beta)$

Using the angle sum identity:

$\rightarrow x_2/x_1 = (\sin \alpha \ \cos \beta + \cos \alpha \ \sin \beta) / \sin \beta $
$\rightarrow x_2/x_1 = \frac{\sin \alpha \ \cos \beta}{\sin \beta} + \cos \alpha $
$\rightarrow x_2/x_1 = \frac{\sin \alpha}{\tan \beta} + \cos \alpha $

Solve for $\beta$:

$\beta = \arctan \left(\frac{\sin \alpha}{x_2/x_1 - \cos \alpha} \right)$

where $\alpha, x_2, x_1$ are given values.

Now that we have $\beta$ we can substitute it into $r = x_1/(\sin \beta)$ to find r.