3

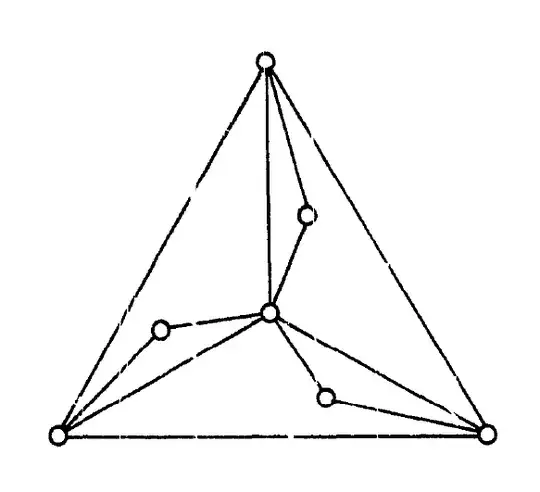The Petersen graph is a famous example of a 1-tough non Hamiltonian graph, and I stumbled across the following graph which also follows the property: (another example).
I found this example in a paper by V. Chvátal. However, I found out that we can extend this graph as so: 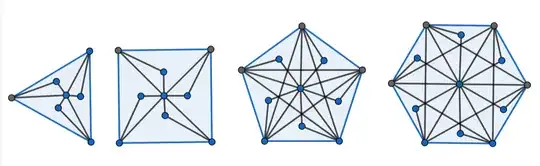(extensions) and that all such graphs will follow this property as well. (Here, all the extended graphs are complete, and thus we can see that the triangle version is just a special case of a complete graph).

Just to be sure, I wrote a code in python to check if these graphs follow the property, and using this 'brute force' method also shows that these graphs are indeed non-hamiltonian and 1-tough. I can't seem to find anything similar anywhere on the internet, and I just know the basics of graph theory, so I wanted to ask if this property is just trivial. Is it just obvious that such extensions of complete graphs will follow this property or could this actually be anything interesting?

Kian Shah
  • 71
  • 2

1 Answers1

1

You are correct that these graphs are all non-Hamiltonian and $1$-tough. I don't know how to debate whether this is obvious or not, but there is a proof that is not just brute force:

Not hamiltonian. Whenever three or more vertices of degree $2$ all share a neighbor, the graph cannot be Hamiltonian. That's because a Hamiltonian cycle must always use both edges out of each degree-$2$ vertex, but at the same time it cannot use more than two edges out of that common neighbor they have.

Tough. We want to delete as few vertices from this graph as possible while separating it into as many components as possible. Here are two observations:

  • We definitely want to delete the center vertex: otherwise, we'll never disconnect the graph, since it's adjacent to everything.
  • After that, the degree-$2$ vertices become leaves, and we never want to delete those: that will never increase the number of connected components, and sometimes it will decrease the number.

So we only need to consider cases where we delete the center vertex, and $k$ "outer" vertices of the complete graph. In this case, $k$ of the degree-$2$ vertices become isolated, but everything else is a single connected component; as a result, we've deleted $k+1$ vertices and only created $k+1$ connected components. This does not violate toughness.

In terms of notability, I think that the very first example was important, because it showed that not all tough graphs are Hamiltonian, and having more examples is less important.

It is nice to have a simple infinite family of examples, but I'm sure that people who think about toughness and Hamiltonicity more than I do already knew that infinitely many such graphs exist. (Otherwise, they'd be asking: what if every tough graph larger than the Petersen graph is Hamiltonian?)

Misha Lavrov
  • 159,700