6

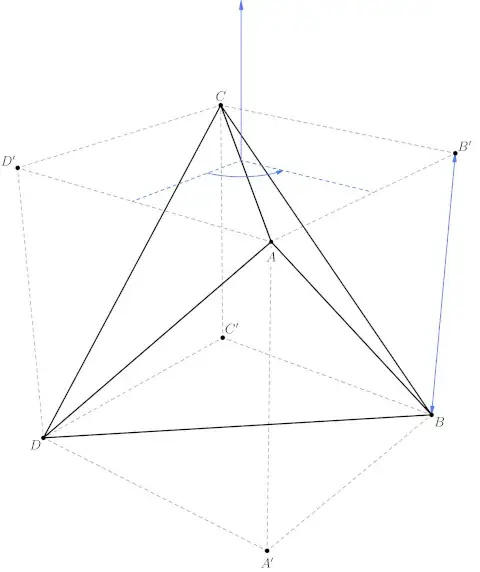
I'm working on an applet that will calculate the product of two symmetries. (It's unfinished but here's a link to the project if you're curious.) I want the applet to show visuals to help the user understand what's happening for each symmetry action -- for example: for rotations, it displays the axis of rotation; for reflections, it displays the plane of reflection.

There are six symmetries which I can't figure out a visualization for. I believe they're called "roto-rotations" or "inversions," but I can't find much information online about them (in my applet they're currently labeled $φ_1$ through $φ_6$). They are the following elements of $S_4$:

(2341), (2413), (3142), (3421), (4123), (4312)

Can anybody help me figure out how these elements can be visualized on the tetrahedron through axes of rotation/planes of reflection/some other visual?

Evyenia Coufos
  • 306
  • This might be pull-through modifications where 3 points in any of the triangular faces are kept and the 4th point is moving through the center and through the center of that triangle to the opposite side. Plays some role in the methane roto-vibration spectrum. – R. J. Mathar Nov 08 '23 at 17:55
  • 3
    It doesn't make sense to ask for closing this well written interesting question. – Jean Marie Nov 08 '23 at 18:50
  • 2
    Welcome to MSE! <> If we embed the tetrahedron as "alternate vertices" in a cube centered at the origin, these symmetries are a quarter-turn about a coordinate axis followed by reflection in the plane orthogonal to the axis. (Three choices of coordinate axis, two choices of quarter-turn, six $4$-cycles in all.) I don't see a "simpler" way to describe them, however; they're not of themselves either rotations or reflections. – Andrew D. Hwang Nov 08 '23 at 20:44
  • 1
    If you are interested in visualizing group theory more generally you may find of interest various graphical depictions of cyclic groups via star polygons and roulette curves ("spirographs"), which lend much visual insight (and may appeal to your artistic side), e.g. see here and here. – Bill Dubuque Nov 08 '23 at 22:52
  • https://en.wikipedia.org/wiki/Improper_rotation – mr_e_man Dec 12 '23 at 16:03

1 Answers1

3

To expand my comment:

A regular tetrahedron inscribed in a cube, and a transformation cyclically permuting its vertices

We've embedded a regular tetrahedron as "alternate vertices" in an axis-oriented cube centered at the origin, and labeled the cube's vertices as shown, with vertical edges $AA'$, $B'B$, $CC'$, and $D'D$.

The indicated quarter-turn about the vertical axis cyclically permutes the edges $(AA'\ B'B\ CC'\ D'D)$ and maps our tetrahedron $ABCD$ to the "other" tetrahedron $A'B'C'D'$.

Reflection in the horizontal plane exchanges each primed-unprimed label pair, again swapping $ABCD$ and $A'B'C'D'$.

The composition is therefore a symmetry of $ABCD$, and effects the cyclic permutation $(A\ B\ C\ D)$ of vertices.

The rotation and reflection commute, and the composite transformation has block-diagonal standard matrix. Here, for example, the composite transformation has standard matrix $$ \left[\begin{array}{@{}rr|r@{}} 0 & -1 & 0 \\ 1 & 0 & 0 \\ \hline 0 & 0 & -1 \\ \end{array}\right]. $$ There are six such matrices because we have three choices for the rotation axis, and then two choices of quarter-turn. In terms of entries, we can change the sign of the $2 \times 2$ block, and simultaneously permuts rows and columns cyclically. This agrees with the count of six $4$-cycles in the symmetric group.

No such matrix is a rotation (the determinant of the standard matrix is $-1$, i.e., the transformation reverses orientation), and neither is it a reflection (because the transformation is not its own inverse). Unlike the situation in the plane, not every orthogonal transformation of three-space is a rotation or a reflection.

Andrew D. Hwang
  • 82,053