1

The so-called hoof is constructed by taking a cylinder enclosed in a cube and a slice from an edge of the cube to the diameter of the cylinder, as shown in the first figure below. About 2200 years ago, Archimedes determined that the volume of the hoof is one-sixth the volume of the enclosing cube. You can find a full description of the problem and its solutions in this paper.

Now, you've probably known since grade school that the volume of a cylinder is $V=\pi r^2h$ and you would expect that any fraction of that volume would be dependent upon $\pi$. So what happened to $\pi$ in the volume of the hoof?

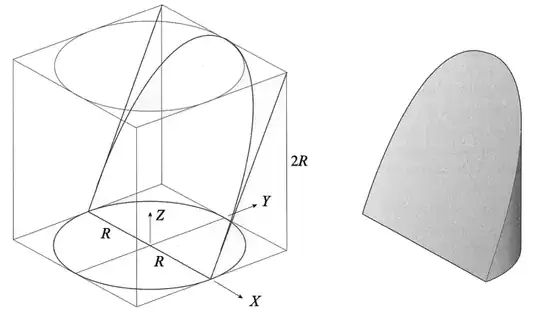
hoof geometry

Cye Waldman
  • 8,196
  • Another solution using calculus here – user170231 Nov 03 '23 at 04:38
  • This may sound a little silly, but isn't the fraction itself a multiple of $1/\pi$. It need not be a rational number. Right? –  Nov 03 '23 at 06:42
  • Whether or not a volume of cut-sections like these is a multiple of $\pi$ is a question of greater interest, I suppose. May be you can study more on these and generalise the question which adds to its current beauty. –  Nov 03 '23 at 06:54
  • @user170231 There are several calculus solutions in the linked paper. I've also done many calculations for non-circular cylinders. – Cye Waldman Nov 03 '23 at 14:45
  • Volume of a cylinder should be $V=\pi r^{2}h$ – Amos C N Nov 07 '23 at 12:58
  • @AmosCN Thanks for catching that. I will correct this. – Cye Waldman Nov 07 '23 at 16:15
  • Fixing a cube length $a$, the volume of the inscribed cylinder is $\pi a^3/4$, so I assume you'd expect rational multiple of $\pi a^3$. I don't know why you would expect that, though. Simply by changing height of the cylinder, by continuity we can get any volume in the segment $[0,\pi a^3/4]$, most of which are not rational multiples of $\pi a^3$. In fact, being a rational multiple of $a^3$ is equally unlikely to happen. – Ennar Nov 07 '23 at 16:38
  • @Ennar I think you are missing my point. If you took a cylinder and took some random piece from it, you'd have $\pi$ in the volume. In order to end up with a volume that is integer or rational you would have to miraculously slice off a piece of infinitely precise dimension. In your example, you might choose $a$ = the inverse cube root of $\pi$. Good luck with that. – Cye Waldman Nov 07 '23 at 16:50
  • @CyeWaldman you are missing my point. If you take random piece, you won't have $\pi$ in the volume. In fact, as I said, to pick a rational multiple of $\pi$ in $[0,\pi a^3/4]$ is as likely as to pick rational number from $[0,\pi a^3/4]$. – Ennar Nov 07 '23 at 16:51
  • @Ennar Of course you would, the volume of the random piece would be a transcendental number because of the $\pi$, hence some multiple of $\pi$. – Cye Waldman Nov 07 '23 at 16:55
  • 1
    @CyeWaldman, what's the cardinality of the set ${ r\pi\in[0,\pi a^3/4] \mid r\in\mathbb Q}$? – Ennar Nov 07 '23 at 17:35
  • $1/6$ is a multiple of $\pi$ too -- although not a rational multiple. – David K Nov 07 '23 at 18:04

1 Answers1

2

If you were to take a random piece of a cylinder -- for example, a wedge of random central angle -- the probability of getting a rational volume would be zero, because the rational numbers in the possible range of volumes are countable whereas the real numbers in the possible range of volumes are uncountable.

But likewise the rational multiples of $\pi$ in that same range of volumes are countable, so the probability of getting a rational multiple of $\pi$ is also zero.

In fact you're not looking at a random piece of a cylinder; you're looking at a piece that was constructed in a very particular way. When you do this, you can get effects that "cancel out" a factor of $\pi$.

In this case the phenomenon is that due to the scaling of the triangles as you take cross-sections from one end of the diameter to the other, as illustrated in the paper you cited.

If we were taking these cross-sections from a half-cylinder, the cross-sections would be rectangles of a fixed height and varying widths, and the areas of the rectangles would vary in proportion to the width, which is simply the $y$ coordinate of the graph of the function $y = f(x) = \sqrt{r^2 - x^2}$, which is a semicircle. So the volume is simply the height of the half-cylinder times the area of that semicircle.

In the hoof, on the other hand, the cross-sections are right triangles of the same width as the rectangles in the previous paragraph, but the heights of these triangles also vary in proportion to their widths, so the area varies in proportion to the square of width, that is, in proportion to the function $y = g(x) = r^2 - x^2$. The graph of that function is a parabola rather than a semicircle, and the area under it does not have the factor of $\pi$ that the semicircle introduces.

So one answer to the question of where the $\pi$ went is that it went into the region between the semicircle and the parabola, and cutting that particular area off the semicircle -- corresponding to cutting off the very particular volume we removed from the half-cylinder to make the hoof -- reduces the area (and volume) from $\pi/2$ times some rational multiple of $r$ to $4/3$ times some rational multiple of $r$.

Compare Volume bounded by cylinders $x^2 + y^2 = r^2$ and $z^2 + y^2 = r^2$, in which we have the intersection of two cylinders. Again there is no $\pi$ in the formula for the volume. In that case it's because the formula for the volume of the sphere has only one factor of $\pi$ in it, and the intersection of the two cylinders gives you something larger than a sphere by a factor of $4/\pi$.

David K
  • 108,155