1

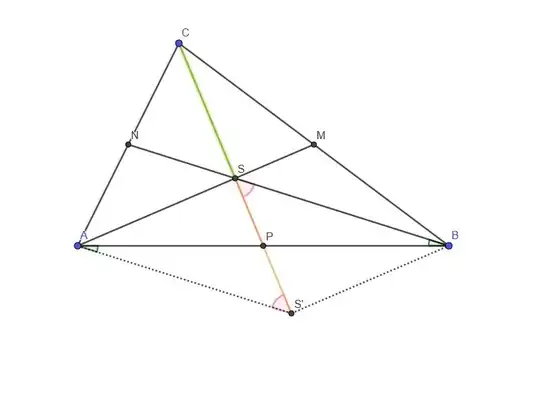
$Q$- From the medians of $\Delta ABC$ one can construct a triangle , the area of which is $\frac{3}{4}$ of the area of $\Delta ABC$.( Problem Solving Strategies, Pg-$318$)

Solution- Let $|ABC|=F$. Reflect the centroid $S$ at the midpoint $P$ of $AB$ with image $S’$. Then $|AS|=\frac{2}{3}m_{a},|SS’|=\frac{2}{3}m_{c},|AS’|=2|RS|=\frac{2}{3}m_{b},|AS’S|=\frac{1}{3}F(since |ASP|=\frac{1}{6})$. Stretch $\Delta ASS’$ from $A$ with factor $\frac{3}{2}$. It’s area increases by factor $9/4$. The stretched triangle $ATQ$ has sides $m_{a},m_{b},m_{c}$ and area $|ATQ|=\frac{9}{4}.\frac{1}{3}|ABC|=\frac{3}{4}|ABC|$. The triangle $ATQ$ can be constructed by the translation of $m_{a},m_{b},m_{c}.$(pg-323)

I am unable to understand the solution so can anyone please show a geometric diagram of the given problem. Thank you

Reza Rajaei
  • 6,236
Sillyasker
  • 862
  • Draw the diagram yourself. $P,Q,R$ midpoints of $AB,BC,CA$. $T$ is the translate of $P$ by vector $\overrightarrow{CQ}$ (or maybe $T,Q$ swapped, not sure which makes more sense to you). – user10354138 Oct 28 '23 at 07:33
  • 2
    I suggest that you try Geogebra. There are tools to construct each step (reflection, measure lengths and areas). – Isomorphism Oct 28 '23 at 07:33
  • I am sorry but am unable to conclude many things from the given diagram from geogebra . How can $SS’=2/3 $of $m_{c}$ – Sillyasker Oct 28 '23 at 09:20
  • Since $S$ is the centroid and $P$ midpoint of side, we have $SP$ one third of the median and now reflect about $P$. – user10354138 Oct 28 '23 at 13:00

1 Answers1

1

Let's have a figure of the problem and denote the triangle made from $m_a, m_b$, and $m_c$ by $T$. $S$ is the centroid; we have: $$|AS|=2|SM| \implies |AS|= \frac{2}{3} m_a, \\ |BS|=2|SN|\implies |BS|= \frac{2}{3} m_b, \\ |CS|=2|SP|\implies |CS|= \frac{2}{3} m_c.$$ Now, note that $|SP|=|SP'|$ and $|AP|=|PB|$. So, $\triangle APS'$ and $\triangle BSP$ are congruent. Therefore, $|AS'|=|BS|$. Moreover, $|CS|=2|SP|=|SS'|$. Hence, we conclude that $\triangle ASS'$ and $T$ are similar and the ratio of corresponding sides is $\frac{2}{3}.$ Thus,

$$\frac{S_{\triangle ASS'}}{S_T}=(\frac{2}{3})^2=\frac{4}{9},$$

and: $$\frac{S_{\triangle ASS'}}{S_{\triangle ABC}}=\frac{S_{\triangle ASP}+S_{\triangle APS'}}{S_{\triangle ABC}}=\frac{S_{\triangle ASP}+S_{\triangle BSP}}{S_{\triangle ABC}}=\frac{S_{\triangle ASB}}{S_{\triangle ABC}}=\frac{1}{3}.$$

Finally,

$$\frac {S_T}{S_{\triangle ABC}}=\frac{S_T}{S_{\triangle ASS'}} \times \frac{S_{\triangle ASS'}}{S_{\triangle ABC}}=\frac {3}{4}.$$ enter image description here

Reza Rajaei
  • 6,236
  • https://math.stackexchange.com/questions/907934/medians-of-a-triangle-and-similar-triangle-properties and https://math.stackexchange.com/questions/2132395/prove-that-three-medians-divide-a-triangle-into-6-triangles-with-equal-surface-a help you understand the relations between the areas and lengths formed by the medians of a triangle, in case you need more clarification. – Reza Rajaei Oct 29 '23 at 06:54