First of all, three 3D representations of surface $(S)$ with implicit equation :
$$\cos(x_1 - x_2) + \cos(x_1 - x_3) + \cos(x_2 - x_3)=0 \tag{1}$$
the first one in $(0, 2 \pi)^3$ with a main cylindrical hole and 6 little solid corners above (3 above, 3 at the bottom),
the second one in $(-4 \pi, 4 \pi)^3$, displaying as many cylinders as an organ has pipes...
the third one explaining how the 3 upper solid corners are in fact, logically, in continuity with the cylindrical shape. It is illustrated on one of the solid corners by the translation materialized by the green arrow.
(Continuation) In the same way, one can translate the two others solid corners, giving a "sort of" (see edit below) elliptical section. Of course, the same operation can be done at the bottom. In this way, our issue is brought back to the computation of the volume of a slant cylinder, which is equal to its height ($2 \pi$) times the area of its basis with the formula $\pi a b$ if this basis is really an ellipse, an hypothesis we do for the moment.
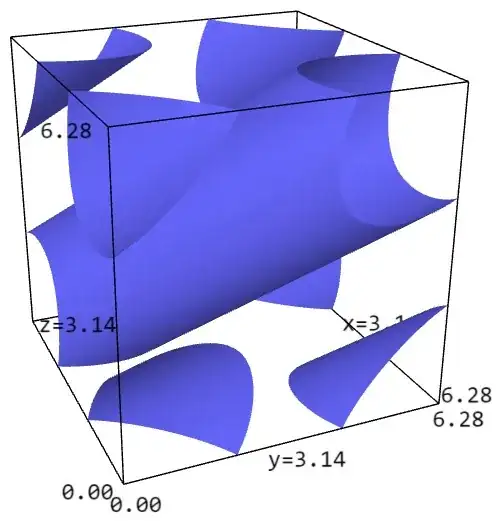
Fig. 1.
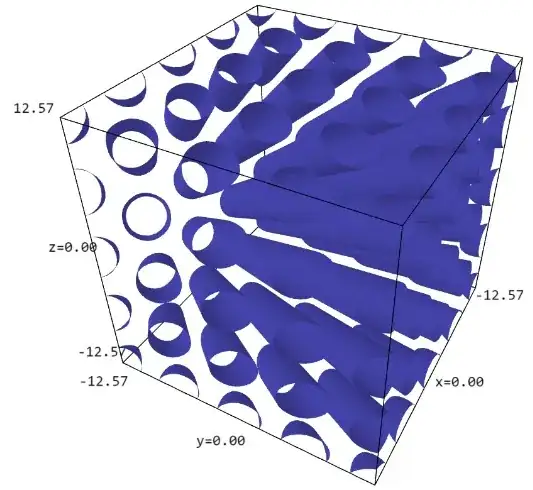
Fig. 2.
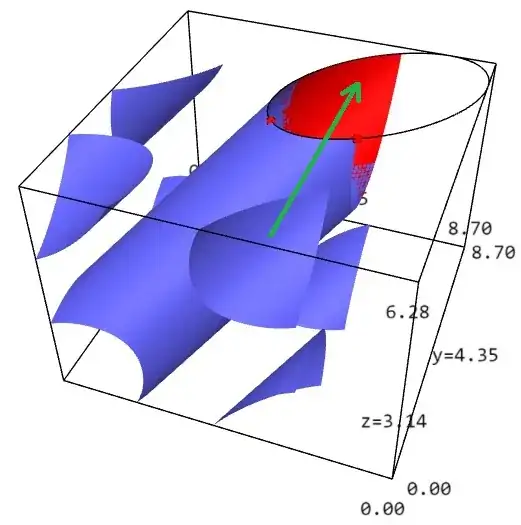
Fig. 3.
The volume we have to integrate is a certain part of the cube $(0, 2 \pi)^3$ (we refer to Fig. 1 in the sequel).
This part can be described as the result of
(i) (Fig. 1) the removal from the cube of a certain cylindrical volume (with axis a big diagonal of the cube) part of a certain "main cylinder" and
(ii) the removal of $6$ little volumic corners (we will call them "chunks") situated in the vicinity of 6 of the 8 vertices of the cube.
Remark : (i) and (ii) come from the fact that the following transformations leave surface $(S)$ invariant :
$T_1 : (x_1,x_2,x_3) \to (x_1+c,x_2+c,x_3+c) $ for any constant $c$.
$T'_1 : (x_1,x_2,x_3) \to (x_1-\pi,x_2-\pi,x_3+\pi)$
and two similar transformations $T'_2, T'_3$ by circular permutation on $T'_1$.
Invariance by transformation $T_1$ justifies the cylindrical shape.
Invariance by transformations $T'_k$ justifies the copy of the main cylinder (its axis passes through the origin and is directed by vector (1,1,1)) into an infinity of cylinders by translations (as can be seen on fig. 2).
Points
$$\begin{cases}P&=&(\frac{2 \pi}{3},\frac{2 \pi}{3},2 \pi)\\Q&=&(2 \pi, \frac{2 \pi}{3},2 \pi)\end{cases}$$
(materialized by red dots in Fig. 3) belong to (S), more precisely to its "elliptical rim".
Under the elliptical hypothesis, it is not very difficult, from the coordinates of $P$ and $Q$ above, to deduce that the elliptical rim has semi-axes $a=\sqrt{2}\frac{2 \pi}{3}$ and $b=\sqrt{\tfrac{2}{3}}\frac{2 \pi}{3}$
Therefore, under the hypothesis, the volume of the slant cylinder is equal to
$$V = H \times A = 2 \pi \times \pi \sqrt{2}\frac{2 \pi}{3}\sqrt{\tfrac{2}{3}}\frac{2 \pi}{3}$$
Last step : this volume has to be subtracted to the volume of the cube, giving the final result :
$$(2 \pi)^3-\sqrt{3}\frac{16\pi^4}{27}\approx 148.069\tag{*}$$
which is close to your result, $\approx 149.188$ but not exactly the same. The reason for that is that our hypothesis of an "elliptical rim" isn't good : it isn't exactly an ellipse.
Edit :
This "would-be elliptical rim" has an equation obtained by setting $x_3=2 \pi$ in equation (1), giving :
$$\cos(x_1 - x_2) + \cos(x_1) + \cos(x_2)=0 \tag{2}$$
Setting
$$\begin{cases}x_1&=&s+t\\x_2&=&s-t\end{cases}\tag{3}$$
(2) can be transformed into :
$$\cos(2t)+2 \cos(s)\cos(t)=0 \ \iff \cos(s)=-\frac{\cos(2t)}{2 \cos(t)}$$
Otherwise said, a quarter of our rim can be described by the cartesian equation :
$$s:=f(t)=\pi- \operatorname{acos}\left(\frac{\cos(2t)}{2 \cos(t)}\right),$$

Fig. 4 : The pseudo elliptical rim curve with equation (2) (black) and the curves associated to functions $f$ and $-f$ (blue) which are the image one of the other through transformation (3) which amounts to a rotation followed by an enlargement with linear ratio $\sqrt{2}$, i.e., area ratio $2$ (as can be seen on the jacobian of transformation (3))/
We must be careful with the domain of definition of this function $f$ ; due to the domain of $\operatorname{acos}$, it is defined for values of $t$ verifying
$$-1<\frac{\cos(2t)}{2 \cos(t)}<1 \iff -2 \cos(t)<2 \cos(t)^2 - 1<2\cos(t)\tag{4}$$
Solving a quadratic equation, condition (4) is equivalent to
$$t \in (-\alpha,\alpha) \ \text{where} \ \alpha=\operatorname{acos}(\frac12 (\sqrt{3}-1))\approx 1.19606$$
Now, the final calculations. Starting from
$$\int_0^{\alpha} f(t) dt \approx 1.96717$$
and that this area accounts for the $1/4$th of the area (see Fig. 4), therefore has to be multiplied by $4$ with a subsequent multiplication by $2$ to account for the magnification given by formulas (3), giving finaly the following volume (analogous to (*) above) ;
$$V \approx (2 \pi)^3- 2 \pi \times 8 \times 1.96717 \approx 149.17$$
your result...
"Sage" program for the figure :
var('x1 x2 x3')
from sage.plot.plot3d.implicit_surface import ImplicitSurface
e=2*pi;b=0;
G=ImplicitSurface(cos(x1 - x2) + cos(x1 - x3) + cos(x2 - x3), (x1, b, e), (x2, b,e), (x3, b,e), plot_points=60);G



