1

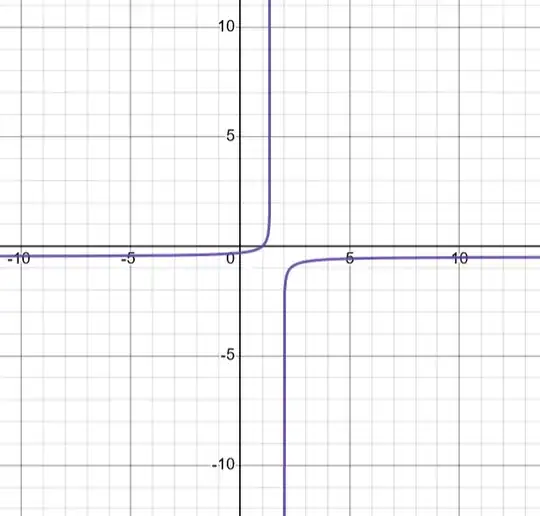
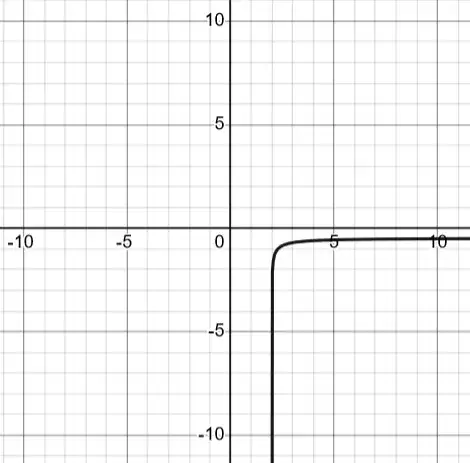
I was investigating the laws of logarithm and playing with Desmos when I realized something curious.

The example equation is $f(x)=\log\left(\frac{2x-4}{6x-8}\right)$ and the graph is this:

enter image description here

The law of logarithms say that: $\log\left(\frac{A}{B}\right)=\log(A)-\log(B)$

Graphing $f(x)=\log(2x-4)-\log(6x-8)$ however shows this:

enter image description here

While the right side of the domain is preserved, the left side of the domain isn't preserved. The reason I thought of is because logs can never take negative values and while $\log(A)-\log(B)$ excludes cases where the numerator and denominator are negative, $\log\left(\frac{A}{B}\right)$ doesn't because $\left(\frac{-A}{-B}\right)=+C$.

However, one thing I noticed is that lots if not all resources about laws of logarithms never mention how some domains will be added/removed if you use this property. I question if this equivalency is still accurate?

Steven Clark
  • 8,744
Just Kirb
  • 11
  • 10
    So long as $A/B,A,$ and $B$ are all within the domain of the logarithm, yes you have $\log(A/B)=\log(A)-\log(B)$. As soon as you start going outside of that, as you have noticed things can go awry. Any rigorous description of the "laws of logarithm" will emphasize this point. – JMoravitz Oct 10 '23 at 15:41
  • Are you assuming that $A, B \in \mathbb{R}$? Because the situation with complex logarithms is more...complex. – Dan Oct 10 '23 at 15:48
  • @Dan Yep, but now I'm now curious on how complex logarithms work, so thanks for bringing it up. – Just Kirb Oct 10 '23 at 15:56
  • @JustKirb: https://math.stackexchange.com/questions/136570/determination-of-complex-logarithm/136659 – Dan Oct 10 '23 at 15:57
  • 1
    @JMoravitz I read more sources and realized on how proofs carefully assume A>0 and B>0 so the equality holds true as it never claims to work for cases where A or B are negative, so thanks for your answer. – Just Kirb Oct 10 '23 at 16:01
  • This WolframAlpha evaluation illustrates there seems to be a problem with Desmos as the imaginary parts of $\log(2x−4)$ and $−\log(6x−8)$ cancel each other out for $x\in\mathbb{R}\land x\notin\left[\frac{4}{3},2\right]$. – Steven Clark Oct 10 '23 at 16:28

0 Answers0