6

Well it's an imaginative and soft question so take it as you wish .

Problem : imagine Spider-man walking on the cantor function (see the plot like the side of a building) :

cantor-function

Now he can throw a line to come faster to the top of the stairs . The problem is the spider-man webs can only solidify on an angle(i.e corner).

Question :

If spiderman have a limitied number of spider-webs which stay only on angle (corner) what is the probability he comes to the top of the stairs on a limited interval of the Cantor's function admitting it's his only means of transport ?

Do you have a strategy ?

I have no attempt because it's a new problem for me but Bernoulli's distribution could be a start .

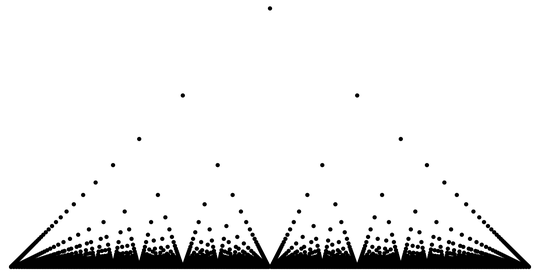
Example of path to come on a horizontal line :

Spiderman-path

The new question is :

Finalizing Question :

If Spiderman is a point on that curve and have the probability $P=1/2$ to get a rational point $(x_i,y_i)$ on the curve he choose (The Cantor set here) and stop if the point is irrational what's the probability he goes at the top of the devil staircase ($x=y=1$) if he is assimilated to an increasing unknow $x$ starting to $x=0$ and $x_i<x_{i+1}$.In other word what's the probability he diverges (projective geometrical point of view) to $x=y=1$ choosing a number of rational point which is bounded ?

We can bound it with the Fréchet-Boole's inequality .

To figure it see :

Circle-ford

Another one and Thomae function

Popcornfunction

The problem can be reformulate in term of Brownian motion :

Spidermanmotion

Simplifying question for kids :

If now a kid plays with a Soap bubble and the bubble in a slight wind goes to a staircase what's chance the bubble don't collapse before the end of the next level of the home?

Reference :

https://en.m.wikipedia.org/wiki/Cantor_distribution

https://en.wikipedia.org/wiki/Fr%C3%A9chet_inequalities

https://en.wikipedia.org/wiki/Ford_circle

https://arxiv.org/pdf/2007.08407v1.pdf

https://arxiv.org/ftp/arxiv/papers/2205/2205.01925.pdf

Barackouda
  • 3,879
  • 2
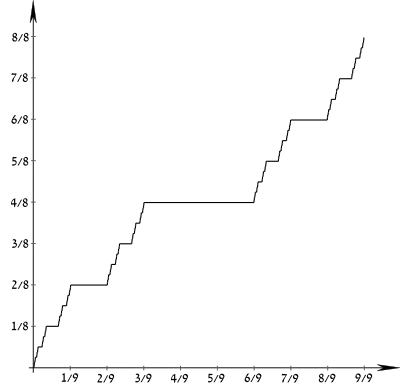
    At the start, the slope is in effect vertical. How does that affect "walking on the Cantor function" and "spider-man webs can only solidify on an angle". What is a "limited interval of the Cantor function"? – Henry Oct 09 '23 at 08:13
  • I guess by 'angle' is meant 'corner' (as these words are the same words in some languages) which would here be the leftmost point of an interval at which the graph runs horizontally. But Erik Satie can better clarify this himself – Vincent Oct 09 '23 at 08:48
  • @Henry a limited interval is $x\in[0,1]$ for example .Spiderman start on a plateau (need to define that ) of the devil's stairs otherwise there no possibility . The problem in standart mathematics is if we have a line $f(x)=ax+b$ starting from a point on an interval $[a,b],0<a<b$ which intersect two extrema (one of the point is a maxima on a subinterval) of the Cantor's function how many line we need to come on a plateau sufficiently large .See https://mathworld.wolfram.com/LineLinePicking.html – Barackouda Oct 09 '23 at 08:52
  • See also Jarvis march https://en.wikipedia.org/wiki/Gift_wrapping_algorithm – Barackouda Oct 09 '23 at 10:02
  • I don't know if I'd call this a soft-question. In my opinion, it's a somewhat squidgy :-) question that needs to nail down what it means, but once it does that, it would seem to have a specific answer. – Brian Tung Oct 11 '23 at 07:21
  • @BrianTung See the edit and thanks for the sophisticate English. – Barackouda Oct 11 '23 at 09:38
  • I put here some question : Do the two events "have a consecutive rational point"and "get a irrational point " dependent ? If so does it works like a "dice probabilstic system" (Bernoulli's distribution) ?If so the form of the dice count so does rational number have a "form" which make it dependent ? – Barackouda Oct 13 '23 at 09:16
  • Well now I think it's not a "soft" question since there is potential depth question see https://arxiv.org/pdf/1203.4141.pdf – Barackouda Oct 13 '23 at 09:40
  • Intruiging idea https://math.stackexchange.com/questions/2209073/is-the-zero-set-of-brownian-motion-homeomorphic-to-cantor-space – Barackouda Oct 18 '23 at 18:13
  • https://en.m.wikipedia.org/wiki/Erd%C5%91s%E2%80%93Ulam_problem – Barackouda Dec 22 '23 at 08:13
  • https://en.m.wikipedia.org/wiki/Propagator#Basic_Examples:_Propagator_of_Free_Particle_and_Harmonic_Oscillator – Barackouda Jan 13 '24 at 09:50

1 Answers1

1

The basis of this answer and the strategy which come with it start :

What is the convex hull of the devil staircase taking only extremal point $P_i$ which is bounded ?

In fact if Spiderman (view as a point) have an illimited numbers of webs Jarvis march is sufficient if we admits there is a limited numbers of point in the convex hull .

Now as it's limited we can refine Jarvis march with Chan's algorithm which is more efficient .

There are other strategy but take it as an example for this problem of computational geometry .

Hope you find something clear and give your feedback.

Edit :

In term of probabilities see Expected number of vertices in a convex hull

From here (p.35) it seems that the probability is equal to $1/2$ is it right ?(false)

See https://people.maths.bris.ac.uk/~matmj/Demislides.pdf and Mahler question .

Using this paper the answer seems to be $P\simeq 1/3^n$ (false too)

I found an partial answer here Continued Fraction and Random Variable

And here "Probability" measures on Cantor set

Edit :

If we consider the term "equiprobable" so the answer is $1/2$ see

Thou shalt not say “at random” in vain: Bertrand’s paradox exposed

See theorem 5.1 Tchernoff bound here

Barackouda
  • 3,879