Why Do Fewer Points Result in Larger Variances?

Question

In school, we are usually taught the following point:

• If you have few data points, if you calculate the variance of these data points, the variance will be very large
• As the number of data points increase, the variance will become smaller

Supposedly, this is justified by the "Consistency" property of estimators. That is, since the Variance is "statistically consistent" - as the number of points used to calculate the Variance increases, it will become closer to the "true value" (Show that sample variance is unbiased and a consistent estimator)

This being said, I have the following question:

Suppose someone wants to measure how many baskets I can score in basketball from the three point line. Since I am not a basketball player, I am likely to miss a lot of shots. However, suppose I luckily happen to score 4 times out of the first 5 times - in this situation, my variance would be quite small. But the more I shoot, I start to miss more baskets and then my variance increases.

Thus, in this case, it is possible that fewer data points might underestimate the true Variance.

This being said, can someone please explain why the variance calculated on a small number of data points is always believed to be much larger than the actual variance ... when in fact it could be smaller than the actual variance?

Thanks!

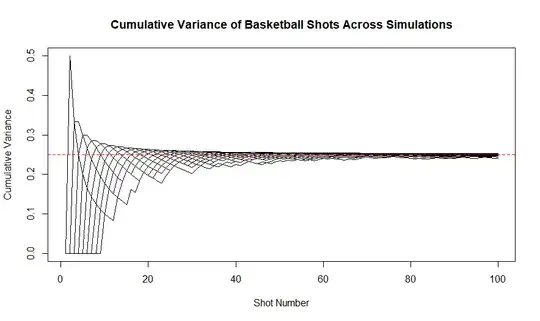
EXTRA: An R simulation which shows the cumulative variance of a basketball being shot 100 times with success probability = 0.5 (i.e. variance of first n shots, first n+1 shots, first n+2 shots, etc.). This entire simulation is then repeated 100 times and then visualized. Note that the variance after the first shot is always 0 (I am not sure if this is correct).

n_shots <- 100
prob_success <- 0.5
n_simulations <- 100
cumulative_variances <- matrix(nrow = n_shots, ncol = n_simulations)
set.seed(123)

for (i in 1:n_simulations) {
shots <- rbinom(n_shots, 1, prob_success)
cumulative_variances[,i] <- sapply(1:n_shots, function(j) if(j > 1) var(shots[1:j]) else 0)
}
plot(1:n_shots, cumulative_variances[,1], type = "l", ylim = range(cumulative_variances),
     xlab = "Shot Number", ylab = "Cumulative Variance",
     main = "Cumulative Variance of Basketball Shots Across Simulations")
for (i in 2:n_simulations) {
  lines(1:n_shots, cumulative_variances[,i])
}
abline(h = 0.25, col = "red", lty = 2)

Answer 1

There are a lot of unstated assumptions in your question, which is what is leading to your confusion.

First of all, what does it mean to say "the variance of these data points?" One meaningful interpretation is that each data point is a realization $x_i$ of some random variable $X$ that obeys some underlying distribution. If we assume that these are independent and identically distributed, then the aforementioned variance might refer to the sample variance $$S^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar X)^2,$$ which is an estimator of the variance $\operatorname{Var}[X]$ of the random variable $X$. But because $S^2$ is itself a random variable, it has a distribution and its own variance.

As a concrete example, suppose $X \sim \operatorname{Normal}(\mu,1)$. Then the sample variance $S^2$ is estimating the variance of $X$, which is $1$. If you took "many" independent observations $x_1, x_2, \ldots, x_n$ of $X$, and you computed $s^2$, you would find that this value will be roughly $1$.

But what does this actually mean? Does it mean that when $n$ is small, $S^2$ is guaranteed to be larger than $1$? No. For instance, you could have observed the sample

$$(3.2, 3.1, 3.4, 3.0).$$

The variance in this case is $s^2 \approx 0.0291667$. If you observed more data, the sample might look like this:

$$(3.2, 3.1, 3.4, 3.0, 1.7, 4.1, 3.8, 2.7, 2.2, 1.5, 5.0).$$

And now the variance is $s^2 \approx 1.06855$. And if you continued to observe more data, you might get something else. The point is, your statement cannot be universally true because, as I have pointed out, $S^2$ is a random variable. Any statement about the tendency of $S^2$ is going to be a probabilistic one.

In fact, it is not difficult to show that this particular estimator $S^2$ is a scale-transformed chi-squared distribution; specifically, $$\frac{n-1}{\sigma^2} S^2 \sim \chi^2_{n-1}$$ where $\chi^2_{n-1}$ is the chi-squared distribution with $n-1$ degrees of freedom. This actually allows us to compute the probability that, for a given sample size, the sample variance is less than the population variance. For instance, for $\operatorname{Var}[X] = 1$ and $n = 4$, we have

$$\Pr[S^2 \le 1] = \Pr\left[\frac{4-1}{1} S^2 \le 3\right] \approx 0.608375.$$ In other words, when a sample of size $n = 4$ is drawn from a normal distribution with variance $1$, the probability the sample variance is less than or equal to $1$ is roughly $0.608375$. That's more than half the time.

What you are really thinking about but not formulating correctly is this idea that the variance of the sample variance decreases as a function of the sample size. That is to say, $\operatorname{Var}[S^2] \to 0$ as $n \to 0$. This we can show is true for normally distributed data, since we already mentioned that $\frac{n-1}{\sigma^2} S^2$ has a chi-squared distribution, hence its variance is

$$\operatorname{Var}\left[\frac{n-1}{\sigma^2} S^2\right] = 2(n-1).$$

Therefore, $$\operatorname{Var}[S^2] = \frac{2(n-1) \sigma^4}{(n-1)^2} = \frac{2\sigma^4}{n-1},$$ and this tends to $0$ as $n \to \infty$.

But this is not true in the case of all distributions, and this is where you've made another unstated assumption. For example, if $X$ followed a Cauchy distribution, the estimator $S^2$ will not converge with increasing $n$.

Answer 2

The Crux of this Query is the confusion over "variance" & "variance of variance" !

At the end of the Post , I will re-write what OP has written , to make it Accurate & Correct.

When we have some Data Points with unknown ( but Constant ) variance & we want to Estimate that variance , then we can choose some Sample Data Points to make our calculations.

When we choose very few Points ( eg $n=3$ ) out of the whole Data Points ( eg $m=1000$ ) then the error between Inherent variance $\sigma_0$ & Calculated variance $\sigma_n$ will be large. It may or may not be true that $\sigma_n$ will be large.
The Estimation will not be accurate.

When we use more Data Points ( eg $n=200$ ) , we will get smaller error between Inherent variance $\sigma_0$ & Calculated variance $\sigma_n$ which will tend to converge. It will not necessarily give smaller $\sigma_n$ in general.
The Estimation will be more accurate.

Eventually , when we use all Data Points ( eg $n=1000$ ) , we will get ZERO error between Inherent variance $\sigma_0$ & Calculated variance $\sigma_n$ where we have the converging Case.
The Estimation will be very accurate.

This is what you are observing with the R CODE.
The Calculated variance is not converging to ZERO , It is converging to $0.25$ which is the Exact theoretical value !
We can check that the error between Inherent variance $\sigma_0$ & Calculated variance $\sigma_n$ is indeed converging to ZERO !

Here is the Correct way to state what OP is trying to state :

OP : "|If you have few data points, if you calculate the variance of these data points, the variance will be very large|"

Make it : "|If you calculate the variance ( out of large Date Set ) with few data points , the error in the variance Estimate will be very large|"

OP : "|As the number of data points increase, the variance will become smaller|"

Make it : "|As the number of data points used ( out of large Date Set ) increases , the error in the variance Estimate will become smaller|"