Is this operator always contained in the convex hull for closed sets?

Question

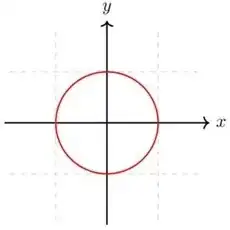
Looking through the window of a bus at night a long time ago I got to think of the following. Given a subset $X\subseteq \mathbb{R}^{n}$ (assume $n\in\mathbb{N}\setminus\{0\}$), define its silhouette $S(X)\subseteq\mathbb{R}^{n}$ as the set of points $p$ such that, for each line (read "ray of light") $l$ in $\mathbb{R}^{n}$ that passes through $p$, $l$ also intersects $X$ (read "is blocked by $X$"). Obviously $X\subseteq S(X)$. Now, the set $D=\{(x,y)\in\mathbb{R}^{2}:x^{2}+y^{2}=1\}$, which I call the donut,

has a silhouette $S(D)=\{(x,y)\in\mathbb{R}^{2}:x^{2}+y^{2}\leq 1\}$, but the silhouette of $S(D)$ itself is again $S(D)$, therefore we cannot tell the donut from its silhouette by looking at their respective silhouettes (meaning that one cannot see the shape of a pastry from its silhouette, pun).

Now, at first I thought that a silhouette would turn out to simply be the convex hull, but that is wildly not true. Consider, if you will, the modified donut $D′=\{(x,y,z)\in\mathbb{R}^{3}:z=0,x^{2}+y^{2}=1\}$: its silhouette is now itself, while the convex hull of $D^{\prime}$ is the unit disc with $z=0$.

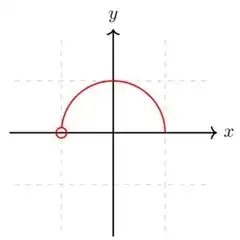
Then, for a long time, I thought, despite their differences, that one could at least prove that the convex hull always contains the silhouette, but recently I found... the croissant. This set, given by $C=\{(x,y)\in\mathbb{R}^{2}:y>0,x^{2}+y^{2}=1\}\cup\{(1,0)\}$

has a silhouette $S(C)=\{(x,y)\in\mathbb{R}^{2}:y\geq 0,x^{2}+y^{2}\leq 1\}\setminus\{(−1,0)\}$, while its convex hull is $\{(x,y)\in\mathbb{R}^{2}:y>0,x^{2}+y^{2}\leq 1\}\cup\{(1,0)\}$ (correct if I am wrong, it has been a long time since I studied analytic geometry): so $(0,0)$ belongs to $S(C)$, but not to the convex hull of $C$.

So, my questions are:

• Is there a standard name for the "silhouette" in the literature, so I can read more?
• More importantly, it appears that the fact the croissant is not closed is vital to prove its silhouette is not contained in its convex hull. So, is the silhouette of a set $X$ necessarily contained in its convex hull IF we assume $X$ is closed? I have no idea of how that could be proven...

Answer 1

First of all let me give a counter-example to your conjecture (based on your croissant adapted to become a closed set whose convex hull is not closed, cf. Are convex hulls of closed sets also closed?). Consider the subspace $W$ of $\Bbb{R}^2$ defined by:

$$ W = \{ (x, y) : \Bbb{R}^2 \mid y = e^x \lor (x = 0 \land 0 \le y \le 1) \lor (x \ge 0 \land y = 0)\} $$

So $W$ (a "wide-mouthed worm") is the union of the graph of the exponential function, a unit segment on the $y$-axis and the non-negative points on the $x$-axis. Then $W$ is closed and its convex hull $C(W)$ and its silhouette $S(W)$ are given by: \begin{align*} C(W) &= \{ (x, y) : \Bbb{R}^2 \mid (x \ge 0 \land y = 0) \lor y > 0\} \\ S(W) &= \{ (x, y) : \Bbb{R}^2 \mid y \ge 0 \} \end{align*}

I.e., the convex hull is the closed upper half-plane with the negative points on the $x$-axis removed, while the silhouette is the whole of the closed upper half-plane. So $W$ is a closed set whose silhouette is not contained in its convex hull.

To get a result along the lines of your conjecture, let's prove that if $n \ge 2$ and $X$ is a subset of $\Bbb{R}^n$ whose convex hull $C(X)$ is closed, then the silhouette $S(X)$ is contained in $C(X)$. Let $x \in \Bbb{R}^n \setminus C(X)$. Then $\{x\}$ and $C(X)$ are disjoint closed convex sets and $\{x\}$ is compact, so by a form of the hyperplane separation theorem, there is a hyperplane $H$ that strictly separates $\{x\}$ and $C(X)$ (i.e., $\{x\}$ and $C(X)$ are disjoint from $H$ and on opposite sides of it). If $L$ is any line through $x$ parallel to $H$, $L$ does not meet $C(X)$, so $x$ is not in $S(X)$. This shows, in particular, that if $X$ is compact then its silhouette is contained in its convex hull, since the convex hulls of compact sets are closed (see copper.hat's answer to Is the convex hull of closed set in $\mathbb R^{n}$ is closed?).

The case $n = 1$ is special. The above argument does not apply because the separating hyperplane is a single point and doesn't contain any lines. In this case, the silhouette of any non-empty set $X$ is the whole of $\Bbb{R}$ and will not be contained in the convex hull unless $X$ is unbounded below and above.